Around 1801, Thomas Young discovered interference of light. This phenomenon is only possible with waves, providing conclusive evidence that light is a wave. In Young’s experiments, light sent through two separate slits results in a pattern that is very similar to the one produced by the interference of water waves shown in Figure 2.
Figure 2 Water waves from two sources interfere with each other to form a characteristic pattern: (a) A ripple tank is a shallow glass tank of water used to demonstrate the basic properties of waves. In it, a shaking paddle produces waves that travel toward a barrier with two slits. (b) Plane waves strike two narrow gaps, each of which produces circular waves beyond the barrier, and the result is an interference pattern.
Let’s spend some time experimenting with water waves before we go on to reproducing Young’s experiments on the interference of light. Start by building a ripple tank, as shown in Figure 3, out of a glass baking pan (for example, a Pyrex® rectangular pan), some wood, two rubber bands, and a vibrating motor made for pagers and cellular phones.
Figure 3 In our home-built ripple tank, a wooden stand supports a glass baking pan a distance away from a white sheet of paper. (a) With a light shining from above, ripples on a shallow layer of water in the pan are projected as shadows on the paper. (b) A small vibrating motor attached to a suspended beam just touching the water surface produces plane waves with which we can conduct experiments on wave reflection, refraction, and interference. For the sake of clarity, these pictures don’t show the steel wool padding that we use to absorb reflections at the tank walls.
The waves in the shallow layer of water are better observed by illuminating them from above to cast shadows through the glass bottom onto a white sheet of paper 50 cm below the tank. Use a spotlight, not a floodlight for illumination. Even better, use a strobe light (like the ones used by party DJs) to “freeze” the waves in place. Fill the pan with water to a depth of around 5 mm, and then fit pieces of metal sponge around the edges of the tank to reduce unwanted wave reflections from the pan’s walls. Test the setup by dimming the room lights and lightly dipping a pencil into the water to create ripples.
To generate continuous plane waves, attach the vibrating motor to a wooden beam. Use rubber bands to suspend the beam from a support beam, and adjust the height of the vibrating beam so that it just touches the water surface. Power the motor from a 1.5-V D cell through a 100 Ω potentiometer (e.g., Clarostat 43C1-100).
Next, set up two straight barriers with a short one between them, along a line parallel to the vibrating beam. Make the gaps between barriers about 1-cm wide. Turn the potentiometer to generate straight waves with a wavelength of about 1 cm. Try different separations between the slits, and see if your data agree with the equation:
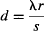
where d is the fringe separation (e.g., between the central fringe and the first fringe to its side), λ is wavelength, s is the distance between the slits, and r is the distance from the 2-slit barrier to the point where the fringes are observed.
Thomas Young did essentially the same thing using colored light instead of water waves. We will use inexpensive laser pointers and a simple double slit to replicate the experiment that Young performed to support the theory of the wave nature of light (Figure 4). Instead of making a double-slit slide,* we use one made by Industrial Fiber-optics. Their model IF-508 diffraction mosaic is a low-cost ($6) precision array of double slits and gratings for performing laser double- and multiple-slit diffraction experiments. The mosaic is mounted in a 35-mm slide holder and contains four double slits and three multiple-slit arrays on an opaque background with clear apertures. Double-slit separations range from 45 to 100 μm in width. The gratings are 25, 50, and 100 lines/mm.
Figure 4 A modern version of Young’s experiment to demonstrate the wave nature of light. (a) All that is needed is an inexpensive laser pointer and a slide with two slits. (b) The separation between fringes is related to the distance between the slits according to d = λr/s. (c) A thin filament of thickness s produces the same interference pattern as a double slit of the same separation.
Interestingly, Young found that the separation between fringes is related to the distance between the slits exactly through the same equation as the water analog:
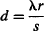
where s is the distance between slits, λ is the wavelength of the light, d is the separation between fringes (the distance between central maximum and each of the first bright fringes to its side), and r is the distance from the slits to the screen.
For the double slit marked “25 × 25” in the IF-508 diffraction mosaic, s = 45 μm. Using red, green, and violet laser pointers with r = 1 m, we measured the fringe separations shown in Table 1.
TABLE 1 Calculated and Measured Double-Slit Interference Distance Between Center and First Bright Fringe for Fringe for s = 45 pm at Different
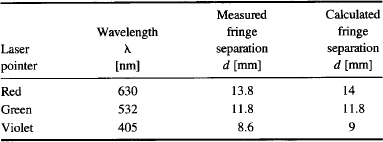
The deviation between measured fringe separation and calculated fringe separation is because of our assessment of the location of the center of each fringe. Better accuracy can be obtained by repeated measurement and averaging. Try out this and other slit separations available in the IF-508 slide (s = 5.8, 7.5, and 10 μm) for yourself, and see how well the wave model accounts for the behavior of light.
Notice that d = λr/s is not dependent on the width of the slits, only on their separation. Interestingly, this same equation works when there are no slits at all. If one shines a laser pointer at a human hair in a dark room, the separation d between the interference fringes can be calculated by making s equal to the diameter of the hair.1 Try it out! Shine a laser pointer at a hair and measure the distance between the interference fringes. Try to calculate the width of the hair—you should come up with a thickness of around 50 to 150 μm. Try to remember this, because the equivalence between a double-slit interference pattern and that obtained using a very thin filament will become very important in experiments that we will conduct later to expose quantum effects.
Leave a Reply