Now that we’ve given away the ending, let’s go back and explore the wave theory of light a bit further. First, we need to establish some basics about wave phenomena. Imagine sitting in a fishing boat on a perfectly calm and windless morning. Then, imagine that a speedboat whizzes suddenly past. Just after lamenting the end of your tranquil morning, you’d notice your boat start bobbing up and down. This happens because the passing speedboat sends a wave across the water. Your boat rises on the wave’s crests and falls in the wave’s troughs.
Now, imagine that an identical speedboat passes by the opposite side at just about the same time. You would then notice that when the crests of the two waves arrive at the same time, your boat bobs twice as high. This is referred to as constructive interference. On the other hand, when a crest of one boat’s waves coincides with a trough of the other’s, your boat doesn’t bob at all. This is called destructive interference. For all cases in between, the height of your boat will be somewhere in between, as determined by adding the heights of the two individual waves.
This method of arithmetically adding wave heights is known by physicists as superposition, a concept we will revisit. More generally, the interaction between multiple waves is called wave interference. And it is one unexpected observation of this effect that allowed the wave theory of light to finally emerge from Newton’s shadow.
DEFINITION
Wave interference is the interaction of two (or more) waves whenever they overlap. Constructive interference occurs when the component waves combine to create an even larger wave; destructive interference occurs when the waves act to cancel each other out.
Superposition is the arithmetic summation of two (or more) waves, such that the total height of the resulting wave at any particular point is equivalent to the heights of the individual waves combined.
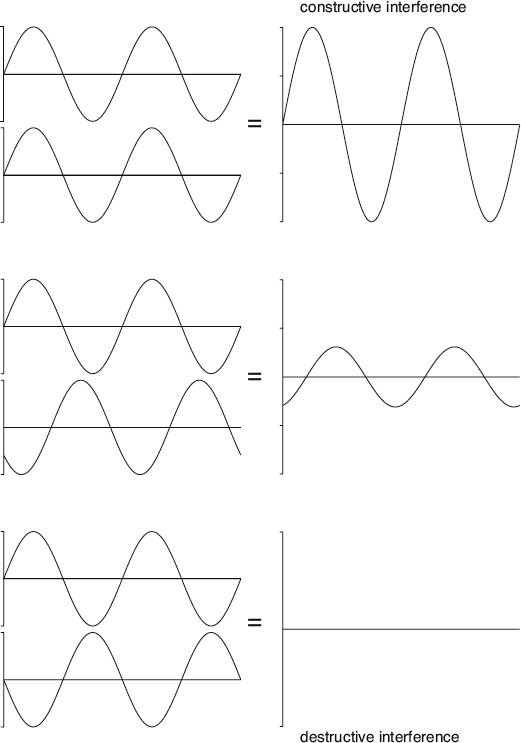
When two waves interfere, the size of the resulting wave depends on whether the crests of the incoming waves arrive at the same time (top), the crest of one wave arrives at the same time as the trough of the other (bottom), or something in between.
What does this have to do with light? Well, imagine now that you are standing in a darkened bedroom and then crack open the door to a lighted hallway. You would expect that a large rectangular shape would light up on the bedroom wall as the light passes between the door and its frame. But what would happen if you closed the door more and more so that the gap between door and frame became wafer thin? At the turn of the nineteenth century one of Newton’s own countryman, Thomas Young, sought to answer exactly that.
QUANTUM QUOTE
It is infinitely more useless, and less ingenious, than the Indian theory of the Elephant and Tortoise.
—An unenthusiastic review of Thomas Young’s experiment by a devotee of Newton, as published in the Edinburgh Review.
To investigate this question, Young cut a tiny pair of slits into an otherwise opaque object and moved it to a darkened room. He directed a beam of light through the slits, and then took a look at what appeared on a screen a few meters away. Instead of seeing two thin stripes appear, as geometric optics would predict, he saw an entire series of stripes line up along the screen like a picket fence. The best explanation for this observation utterly conflicted with the particle theory of light: it was as if light was behaving like a wave.
Young hypothesized that the initial beam was a wave traveling through the room. When it interacted with the two slits (points A and B in his original figure), each slit would act as the source of a new wave—just like the circular pattern formed when water waves pass through a narrow channel. As they move away from the slits, the two waves begin to overlap and interfere with one another. When looking at the darkened screen, the resulting pattern that emerged would be a series of stripes—dark when a crest of one wave meets a trough of the other (points C, D, E, and F), and light where the crests of the two waves coincide.

Young’s original diagram shows the result of his famous double slit experiment: a pattern of overlapping waves.
The technical term for the image Dr. Young saw on his screen is a diffraction pattern. Diffraction patterns can be observed whenever two waves interfere with one another, be they waves of water on a lake or light passing through a narrow slit into a darkened room.
DEFINITION
A Diffraction pattern is the image that appears when two or more waves interfere after passing through a narrow opening; bright stripes emerge in regions where the waves constructively interfere, while dark stripes form where the waves destructively interfere.
Though initially treated with skepticism, Young’s work (along with that of others) gradually gained acceptance. Before long, it had managed to knock Newton’s particle theory of light onto the ropes. The final knockout blow, however, was delivered about a half-century later from the Scottish physicist James Clerk Maxwell.

JAMES CLERK MAXWELL
Unlike Isaac Newton, who was knighted late in life, James Clerk Maxwell acquired no public honors during his relatively short lifetime. This is certainly no reflection of his impact to science, however. His contributions were as important as those of any scientist of his time or before, and even Albert Einstein would later put him on a pedestal side-by-side with Newton.
Born by the name of James Clerk in 1832, he became a Maxwell only after his family inherited an estate of that name. At the tender age of 14, he published his first scientific paper, on the geometry of ellipses. Maxwell was known for his geometric, rather than analytical, way of approaching problems. This preference of shapes to equations is ironic given that he is best known for deriving perhaps the most elegant set of equations in all of physics.
Maxwell’s interests spanned far and wide, and—when he wasn’t busy unifying electricity and magnetism—he explained the stability of Saturn’s rings, dabbled in English literature, explored color blindness, and even performed the first demonstration of color photography.
Leave a Reply