Viscosity, μ is a property of fluid which offers resistance to sheer deformation. Different fluids deform at different rates under the same shear stress. Fluid with a high viscosity, such as lubricant oil deforms more slowly than fluid with a low viscosity such as water.
In any fluid flow, layers move at different velocities and the fluid’s viscosity arises from the shear stress developed between the layers that ultimately oppose any applied force. The relationship between the shear stress and the velocity gradient can be understood as two plates closely spaced at a distance, ∂y, and separated by a homogeneous substance as shown in Figure 9.1. Assuming that the plates are of large area A and that the lower plate is fixed, a force F is applied to the upper plate. If this force causes the substance between the plates to undergo shear flow with a velocity gradient ∂u/∂y, the substance is called a fluid.
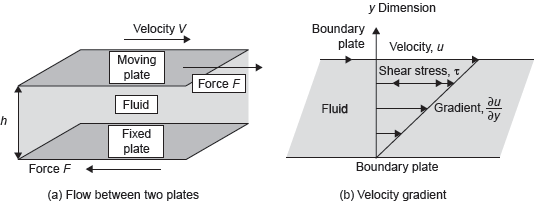
Figure 9.1 Velocity Variation Near Solid Boundary
The applied force is proportional to the area and velocity gradient in the fluid. Combining these three relations results in the equation:
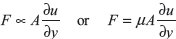
where μ, is proportionality constant called as viscosity.
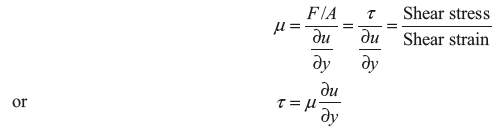
Thus, for straight, parallel, and uniform flow, the shear stress between layers is proportional to the velocity gradient in the direction perpendicular to the layers. This statement is known as Newton’s law of viscosity.
Here, μ is known as dynamic viscosity and its unit is Newton second per square metre or poise (P). The ratio of dynamic viscosity and density of fluid is known as kinematic viscosity (v). Its unit is m2/s. 1 stoke = 10− 4 m2/s.
1 N s/m2 = 10 P and 1 stoke = 10−4 m2/s.
Variations in Viscosity with Temperature: The viscosity of liquid decreases with increase in temperature while viscosity of gases increases with increase in temperature.
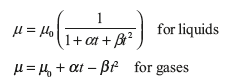
where α and β are constants and t is temperature. μ0 is viscosity at 0°C.
Example 9.1: The dynamic viscosity of lubricating oil used between shaft and sleeve is 10 P. The diameter of the shaft, which rotates at 200 rpm, is 0.5 m. The sleeve length is 100 mm. Calculate the power lost if the thickness of oil film is 2 mm.
Solution:
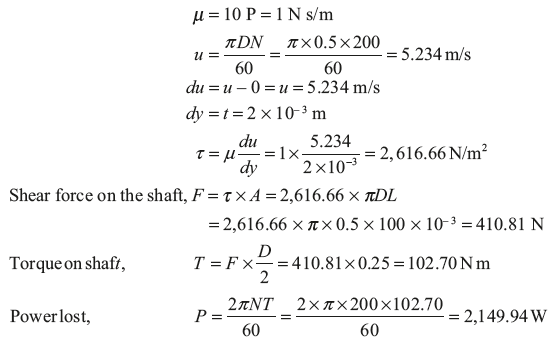
Leave a Reply