The expected value of a random variable tells us something about the location of its distribution, but we need a characterization of dispersion and risk as well. In descriptive statistics, we consider squared deviations with respect to the mean. Here we do basically the same thing, with respect to the expected value.
DEFINITION 6.9 (Variance and standard deviation) The variance of a random variable X is defined as
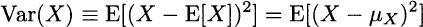
where we have used the shorthand notation μX = E[X]. Variance is often denoted by σ2. Standard deviation a is the square root of variance.
Once again, we note that variance and standard deviation for a random sample are random variables, whereas they are well-defined numbers for a random variable. This is much clearer if we write variance explicitly for a discrete random variable:
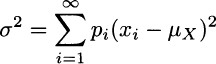
and compare it against variance for a sample consisting of n observations:
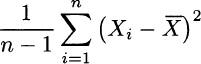
The remarks we made in Section 6.3.1 regarding the expected value apply here as well: The support can be infinite, whereas a dataset cannot, and it takes a lot of knowledge, the whole PMF, to calculate variance. Furthermore, we should raise a couple of issues about variance, which can be better appreciated by thinking about the following question:
We are interested in random fluctuations of weekly demand for the spare parts of a certain item. Variance of this demand is 10,000 items per week, squared. Is this a large or small variance ?
To begin with, variance is an average squared deviation with respect to expected value, but it is hard to think of “items squared.” This is why standard deviation is useful, as it is expressed with the same measurement units as the expected value. In the case above, standard deviation is 100 items per week. However, it is hard to tell if it is actually large. If expected value is 10,000 items per week, uncertainty is almost negligible. If expected value is 250 items per week, that standard deviation is fairly large. This is why sometimes we use the coefficient of variation, defined as
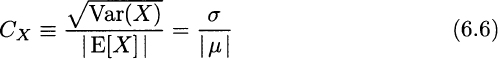
We need to take the absolute value of the expected value, as this could be negative. As a reference point, a variable with a fair amount of variability may have a coefficient of variation of about 1.
Leave a Reply