The diffusivity equation describes the pressure profile in an infinite-acting, radial reservoir, with a slightly compressible and constant viscosity fluid (undersaturated oil or water). This equation, with similar expressions in wide use in a number of engineering fields such as heat transfer (Carslaw and Jaeger, 1959), has the classic form

Its generalized solution is
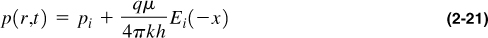
where Ei(x) is the exponential integral and x is given by

For x < 0.01 (i.e., for large values of time or for small distances, such as at the wellbore), the exponential integral –Ei (–x) can be approximated by –ln(γx), where γ is Euler’s constant and is equal to 1.78.
Therefore, Equation (2-21), at the wellbore and shortly after production, can be approximated by (p(r,t) ≡ pwf)
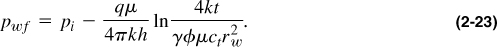
Finally, introducing variables in oilfield units as listed in Table 1-1 and converting the natural log to log base 10, Equation (2-23) becomes
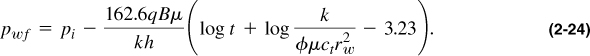
This expression is often known as the pressure drawdown equation describing the declining flowing bottomhole pressure, pwf, while the well is flowing at a constant rate q.
Because a producing well is usually flowing for long times with the same wellhead pressure (which is imposed by the well hardware, such as chokes, etc.), the resulting bottomhole pressure is also largely constant. Therefore, Equation (2-24), which is for constant rate, must be adjusted. More commonly, the constant-bottomhole-pressure situation results in a similar expression, which, although it appears as a mere algebraic rearrangement, is an approximation of the analytical solution to Equation (2-20) with the appropriate inner boundary condition (Earlougher, 1977):
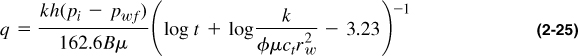
where the time, t, must be in hours.
Equation (2-25), including the skin factor, becomes
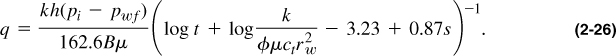
Example 2-3. Prediction of Production Rate in an Infinite-Acting Oil Well
Using the well and reservoir variables in Appendix A, develop a production rate profile for 1 year assuming that no boundary effects emerge. Do this in increments of 2 months and use a flowing bottomhole pressure equal to 3500 psi.
Solution
From Equation (2-25) and substitution of the appropriate variables in Appendix A, the well production rate is given by
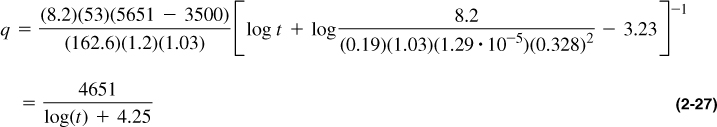
For t = 2 months, for Equation (2-27) the production rate q = 627 STB/d.
Figure 2-2 is a rate-decline curve for this oil well for the first year assuming infinite-acting behavior. The rate decline is from 627 STB/d (after 2 months) to 568 STB/d (after 1 year).
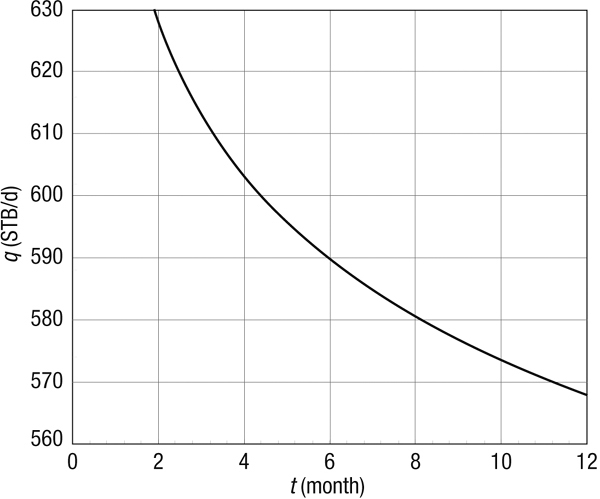
Figure 2-2. Rate decline for an infinite-acting oil reservoir (Example 2-3).
Leave a Reply