Bohr realized that if there is an uncertainty relationship between momentum p and position x:
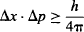
which comes from quantizing momentum as a function of wavelength:
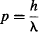
A similar uncertainty principle must then exist between energy E and time t. This is because:
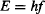
where frequency is the inverse of a time interval f = 1/t, so:
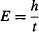
Indeed, an identical relationship exists for the product of the uncertainty in the measurement of a particle’s energy ΔE, and the uncertainty in the measurement of the time Δt at which the particle possesses that energy. The formal derivation of this uncertainty relationship is more complex than deriving the uncertainty between measurements of position and momentum, so we will limit ourselves to stating it as:
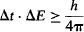
Experimentally proving this form of the Uncertainty Principle is not easy. It requires ultrafast lasers and detectors that are beyond the reach of most casual experimenters’ budgets. However, the uncertainty in frequency measurement of a signal as a function of the signal’s duration is a convenient and educational model of the quantum time–energy uncertainty relationship.
Leave a Reply