In Section 13.1.1 we defined EVPI, which is not only a way to price perfect information, but also a measure of the impact of uncertainty. If EVPI is low, uncertainty is not that relevant in the decision. However, EVPI is in most cases a theoretical construct, as we cannot trade the unpleasing here-and-now decision problem for the reassuring wait-and-see one. In the example above, what we have done is more practical: We assessed the value of solving a stochastic model against the solution of a much simpler deterministic model, based on expected values of uncertain parameters. Here we formalize the concept, using the framework of Section 13.1.1. There, we defined the here-and-now problem
which yields an objective value f* and a decision vector x*.
As we have seen, we could disregard uncertainty and solve a deterministic problem based on expected values. Using a somewhat sloppy notation, let us denote by 
the expected value of the problem data and define the deterministic “expected value” problem
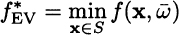
which yields the “expected value solution” 
. This model also yields a value of the objective function, but, as we have seen, the solution must be evaluated within the actual uncertain setting. Doing so yields the expected value of the expected value solution:
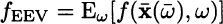
What we should compare is fEEV against f*. The value of the stochastic solution (VSS) is defined as
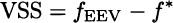
for a minimization problem.21 When VSS is large, the additional effort in generating scenarios and solving the much more complicated stochastic programming effort does pay off. As a final remark, we should note that in this discussion we have taken for granted that the scenario tree describes uncertainty adequately. In other words, solutions are compared in sample. If we do not feel too comfortable with this assumption, we may compare solutions out-of-sample on a much larger set of scenarios. This is also a good way to check the validity of the selected scenario generation approach and the robustness of the solutions that we obtain.
Leave a Reply