In 1925, German physicist Werner Heisenberg was an assistant to Niels Bohr at the Institute of Theoretical Physics at the University of Copenhagen. Heisenberg’s research related to the development of mathematical operations to calculate the expected results of experiments on hydrogen atoms based only on observables—that is, using only quantities that could be experimentally measured, either directly or indirectly, such as electron momentum and position and photon wavelength.
Heisenberg noticed that the mathematical operations involving the position and momentum of the electron seemed to indicate that you could not measure both of these at the same time without a compromise in the precision of the measurements. The math required to solve Heisenberg’s “Matrix Mechanics” baffled the physicists of the time (we certainly don’t intend to put you through it), but there is an easier way of understanding this concept by considering the meaning of various wavefunctions.
Let’s take the simplest one—the simple sine wave of wavelength λ associated with an electron with momentum p, for which according to de Broglie, λ = h/p. This wave extends to infinity just oscillating as a simple sine wave.
What does it mean if an electron has a wavefunction Ψ that is a simple sine that extends to infinity? Well, since |Ψ|2 is the probability of finding the electron at a certain time and position, a wavefunction that is spread throughout space means that the electron could be anywhere. In other words, since the wavefunction has a very precise wavelength λ, we know the electron’s momentum very precisely, but as shown in Figure 102a, we don’t know where in space it is at all.
Figure 102 The probability of finding an electron at a certain position can be calculated from its wavefunction. (a) The electron could be anywhere in space if its wavefunction is a simple sine wave that is spread throughout space. (b) On the other hand, the position of the electron is much more localized for a wavefunction with a probability density |Ψ|2 that peaks at a certain position and rapidly decays to zero elsewhere.
The wavefunction that we need to find an electron at a specific position is one that has a high value at one specific location and is zero everywhere else. For example, Figure 102b shows us the probability density of an electron that can most likely be found in the vicinity of x. However, what would be the mathematical description of this wavefunction, and what would it mean for the momentum of the electron?
To answer these questions, we need to know that waves can be combined to form a new wave. Just like the waves that we explored in our ripple tank. We can take two waves and add them up to form a new wave. The addition, or superposition, of waves is the essence of the phenomenon of wave interference.
Notice in Figure 103a what happens when we add four waves of different frequency, each of which is uniformly spread out in space. The resulting wave is no longer uniformly spread out, but rather is more concentrated in one place, making it more likely to find the electron at a specific place. As shown in Figure 103b, adding the right component sine waves lets us produce an even more localized wavefunction that approximates the one on Figure 102b.
Figure 103 New wavefunctions can be created by adding various simple sine waves of different frequencies and amplitudes. (a) Adding a few sine waves at different frequencies can produce a wave that is more concentrated in a single place. (b) A much more localized wavefunction with a probability density |Ψ|2 (bold dashed line) that peaks at a certain position can be produced by adding many short-wavelength sine wavefunctions together.
The localized wavefunction includes many different wavelengths. That means that the electron has an equal number of probable momentums p1, p2, p3, etc., since each simple sine wavefunction of wavelength λn that we mixed in has an associated momentum pn = h/λn.
As such, a wavefunction that localizes the position of a particle very well must allow for a very large number of possible momentums for the particle. So, whenever we know the position of an electron very precisely, we lose precision in our knowledge of the electron’s momentum. This trade-off between simultaneously knowing the position and momentum of a particle is known as the Uncertainty Principle. Since quantum physics is the physics of Planck’s constant, you may already have a feeling that this constant is at the very heart of the trade-off between simultaneously measuring the position and momentum of a particle, and you would be right! Heisenberg’s estimate was that the product of the uncertainty in the measurement of position Δx, and the uncertainty in the measurement of momentum Δp had to be greater than Planck’s constant h. More rigorous analysis resulted in the modern mathematical statement:
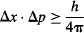
Note that the uncertainties Δx and Δp are not the range of values that x and p can have, but rather the range within one standard deviation of those values.
You will sometimes see the Uncertainty Principle stated as:
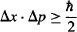
These two forms are identical, because Dirac’s constant 
(pronounced “h bar,” also known as the “reduced Planck constant”) is simply = h/2π. It is commonly used when frequency is expressed in terms of radians per second (“angular frequency”) instead of cycles per second. We don’t want to confuse you with this, but rather wish to make it easy for you to understand what the funny symbol means in papers on quantum physics.
Heisenberg’s Uncertainty Principle was published in a 1927 paper that argued why the position and momentum of a particle cannot both be measured exactly, at the same time, even in theory. For Heisenberg, and later for the whole physics society centered on Bohr’s Copenhagen school, the very concepts of exact position and exact momentum together, in fact, had no meaning in nature.
Please note that the uncertainty in the measurement of either position or momentum is not due to lack of accuracy of our measurement instruments. The compromise in the measurements happens in principle, as a law of nature. That is, even if your measurement instruments are infinitely precise, you cannot simultaneously know the position and momentum of a particle with absolute precision. For this reason, some people prefer to call this concept the Indeterminacy Principle, so that the intrinsic indeterminate character of nature is implied.
Notice, however, that the limitation is in the order of magnitude of Planck’s constant h. In fact, since we are dividing it by 4π, it is one order of magnitude lower than Planck’s constant. This means that the Uncertainty Principle doesn’t really affect our everyday experience, in which momentum is so much larger than Planck’s constant.
Leave a Reply