The missing link in our picture so far is some way to determine the dynamic behavior of particle/waves like electrons, protons, and neutrons. Recall that in order to understand dynamic behavior–that is, how things move and change with time–we need to factor in the impact of forces. Newton’s laws of motion tell us how classical particles react to forces, and Maxwell’s equations perform a similar function in the case of electromagnetic forces acting on a macroscopic scale. But as we have seen, the quantum realm is different, so we are going to need a different governing equation.
Without further ado, courtesy of Erwin Schroedinger, here it is:
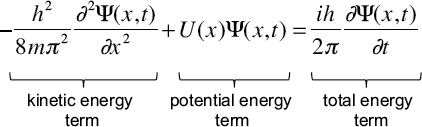
We should say right away that Schroedinger’s equation is a tool used to understand how a particle’s wave function changes at different points in space and how it evolves over time. When physicists “solve” the Schroedinger equation for a particular particle interacting with a particular physical system, they end up with the wave function for that particle (among other things). From this, they can predict the probability of locating the particle at any point in space and any time in the future.
Schroedinger’s wave equation actually comes in many forms. This particular form only deals with a single dimension in space (here called x), even though we know that the space we live in actually has three dimensions. One dimension is plenty for us at the moment. This is also called the time-dependent form of the wave equation, to distinguish it from another form in which the time dependence of the functions has been removed. It turns out the time-independent form is sufficient for dealing with all of the states that will describe atoms, but we don’t need to concern ourselves with this distinction.
Let’s start with the basics. Schroedinger’s equation is an equation, which means the content left of the equals sign is equivalent to the content right of the equals sign. When all is said and done, the math must work out so that the two sides have the same value. Equations can be very simple. 5 + 3 = 8 is an equation. You may have used algebraic equations to solve for unknown numbers, such as 4x – 2 = 7 + x. Schroedinger’s equation is just a more complicated example of the same idea.
Now, let’s identify the terms in this equation. As usual in equations like this, when terms are written right next to each other, it means that they should be multiplied together. The object of this equation is the wave function of a particle, which is represented by the funny Greek letter psi (Ψ). This symbol represents the wave function of a particle as we described. For a given particle in a certain situation, Ψ has a definite value for every location x and every time t. Mathematically, we say that Ψ is a “function” of x and t, and it is often written as Ψ(x,t) to remind us of that.
Next, a few constants appear in this equation, in particular, Planck’s constant (h) shows up twice. The important thing for our purposes is that it is a constant, a number that does not change with the two independent variables x and t. The same goes for the mass (m) of the particle, another constant in the equation.
The lower case i is also a constant, but a peculiar one. This is the symbol we use for the imaginary number equal to the square root of -1. Why? Well, because it is very useful to have a number like that. For all real numbers, positive or negative, when you multiply a number by itself (squaring it) you always get a positive number. But if you multiply i by itself, you get the result -1. Numbers that are combinations of imaginary and real numbers are called complex numbers. It turns out that using complex numbers for wave functions is essential for getting everything to work right. (Again, refer to Appendix C for a more in-depth discussion of imaginary numbers.)
DEFINITION
A real number is an “ordinary” number (like 1, 2, or 3.1415), the square of which is always a positive number.
An imaginary number yields a negative number when squared, since it is formed by a real number multiplied by the square root of negative one (which is abbreviated by the symbol i).
A complex number is formed by any sum of one real number plus one imaginary number.
The capital U stands for the potential energy of the particle. This is the same potential energy we described qualitatively. That’s why the second part is called the “potential energy term.” Recall that it is also a way of describing the effect of a force, or a force field, on a particle. Thus, the presence of U is the crucial link between forces and the behavior of quantum particles.
If the strength of a force varies with position, there is a corresponding potential energy that also varies with position. The “shape” of the force in space is what we usually mean by a force field (like the gravitational or electromagnetic fields). What’s more, the potential energy function contains all of the information needed to completely determine the force. In our one-dimensional, time-dependent form of the Schroedinger equation, U is a function of location (x) only, not of time.
DEFINITION
Potential energy is a position-dependent energy associated with any conservative force. When a potential energy is defined for every point in space, the force is in the direction that corresponds with the most rapid decrease in potential energy.
The four fundamental forces in nature (gravity, electromagnetism, plus two more that we’ll formally introduce) are just the sort of forces which can be described by potential energy functions. Any apparent “force” that we feel in our everyday lives, is derived from one of these four. Recall, for example, our discussion. How the force exerted by your armchair on your backside is due to the electromagnetic force, which is balancing the pull of gravity to keep you from plummeting to the center of Earth.
The four fundamental forces obey the law of conservation of energy and they vary with position. The gravitational force, for example, gets weaker in a predictable way as the separation between two masses is increased. The electromagnetic force gets stronger as a magnet gets closer to a piece of steel. If you’ve ever stuck a piece of preschool artwork to your refrigerator, you have direct experience with this. These are the qualities that make the potential energy U an excellent stand-in for forces in the Schroedinger equation.
Leave a Reply