It is not possible to predict exactly where any individual photon (or electron) will land after traversing the double slits. But since we observe a striped pattern, we can say that the probability of seeing a photon must be higher at certain positions than at others.
The probability is high where the amplitude of the resultant electromagnetic wave, formed by the two waves emanating from the two slits, is high due to constructive interference. The probability is low where the resultant wave’s amplitude is low due to destructive interference. To be more precise, the probability is proportional to the intensity of the light, which is proportional to the square of the resultant wave’s amplitude.
The parallel interpretation for matter is that matter waves somehow represent the probability of finding a particle at a given location. One big difference between matter waves and light waves, however, is that matter waves are described using imaginary numbers. (For a brief introduction to imaginary numbers, refer to our Mathematics Supplement.
It is a fact of nature that properties described by imaginary numbers cannot be directly observed. Thankfully, the square of an imaginary number is a real number, which can be observed. The important point for now is that the square of a matter wave’s amplitude at a certain point, just like the square of an electromagnetic wave’s amplitude at a certain point, gives the probability of locating the particle at that point.
It is only logical that the value of the matter wave’s wave function can’t give us a probability of finding the particle. In order for destructive interference to happen, the wave has to oscillate between positive and negative values. You can have more or less probability, or zero (meaning no chance of something happening), but negative probability has no meaning. That why it makes sense for us to deal with the square of the wave function’s amplitude, which by definition must be positive.
This interpretation—that the square of a particle’s wave function at a point in space and time is equal to the probability of finding the particle at that point in space and time—is attributed to the German physicist Max Born. For this reason, it is often called the Born interpretation. Strictly speaking, the square of the wave function represents the probability of finding the particle in a tiny region (or volume) of space, something we call probability density.
DEFINITION
Probability density is the probability per unit volume in three-dimensional space of finding a particle at that point in space.
You can think of probability density just like mass density in an object whose mass is not evenly distributed. Earth, for example, has a very light atmosphere that surrounds a heavier crust that surrounds a very dense core. If you could travel from the stratosphere to the center of Earth, the mass per unit volume that you would detect would rise along the way. Likewise, the probability of finding a particle per unit volume is highest where the probability density is highest.
While we used to think of a particle as having only a single location, now we must imagine it as extending out in all directions. In general, it is not evenly distributed through the volume it occupies, but is more likely to be found in some places than in others. The places where it is more likely to be found are the locations with higher probability density.
Fortunately, it is possible to construct a matter wave that is more localized to a certain point in space. The trick is that you need to construct it by adding together a few sine waves having slightly different wavelengths.
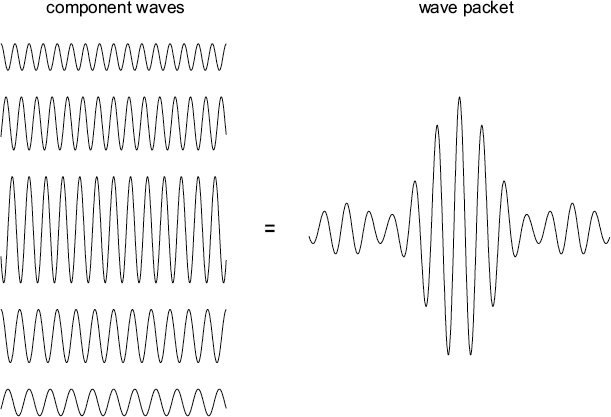
If we add together a few sine waves with varying wavelengths, the result is a wavy function that is “localized” at a certain point in space.
The wave packet in our illustration is most likely to be located at values near its center. But it also has some probability of being located at positions just to the right and left of center. As the particle moves about, its position is therefore only approximately defined. The figure only shows the wave function in one dimension, but in reality it would also extend itself in the other two dimensions of space.
DEFINITION
A wave packet describes a wave that is localized to a certain extent in time and space, i.e., one that has zero amplitude everywhere except around a specific location. The size of a wave packet can vary in all of its dimensions, and its shape can also change as it moves in time.
Leave a Reply