In 1905, Albert Einstein took Planck’s proposal one step further by stating that light itself is a beam of discrete packets, like bullets from a machine gun. Einstein needed this assumption to resolve another troublesome inconsistency in physics, this one concerning the photoelectric effect, by which electrons may be ejected from a metal surface illuminated by light.
Heinrich Hertz observed in 1887 that the minimum voltage required to draw sparks from a pair of metallic electrodes was reduced when they were illuminated by UV light from a mercury vapor lamp (Figure 24a). You may remember that in the same year Hertz confirmed the electromagnetic-wave nature of light. As such, it was no surprise to him that the energy carried by a light wave could shake electrons loose from an electrically-charged piece of metal.
Figure 24 The photoelectric effect was first reported by Hertz. (a) He noticed that sparks could be drawn from an electrode at a relatively low voltage when illuminated by UV light from a mercury lamp. (b) Similar to a rope bridge, a wave of sufficient amplitude was thought to be able to shake electrons loose from the metallic surface.
Take a look at Figure 24b and imagine the following situation: you are on a secret mission in the Amazon jungle. Your arch-enemy shows up as you perilously make your way through a rope bridge over piranha-infested waters. He starts to shake the bridge as you hold on for dear life. After some effort on your nemesis’ part, the bridge will oscillate with such high amplitude that you will plunge to the cliff below. Fortunately, you remembered to pack a parachute and a bottle of piranha repellant …
Just as in this analogy, the wave theory of light would predict that the intensity of the light should determine if the light can generate these photoelectrons. This is because in the wave theory of light, intense light has more energy, and energy is what is needed to liberate the electrons from the metallic surface. Conversely, if the light is dimmed, a point should be reached at which the energy of the wave is too low to kick any electrons away from the metallic electrode.
Also like in the bridge analogy, the wave would take its time to build up sufficient strength to counteract the grip of the metal on its electrons. It would thus take some time after the electrode is exposed to light for it to start expelling electrons. After all, the wave energy is spread over a wide area, so it should take a long time for any one electron to be ejected.
Lastly, ignoring resonances and similar effects, it’s not the frequency at which the bridge oscillates, but rather its amplitude that would cause you to lose your grip and fall. In the same way, the classical wave theory of light would predict that the emission of the electrons is dependent on the intensity of the light, not on its color.
Counter to classical wave theory however, experiment had shown that the intensity did not matter to the ability of light to release electrons from metal. All that mattered was the wavelength of the light. Long-wavelength light could not generate photoelectrons, even if the light was very intense. On the other hand, short-wavelength light could produce photoelectrons, even if the light was of very low intensity. Moreover, electrons are ejected as soon as the light shines on the metal.
In other words, if the light is too red, no electrons are ejected, no matter how bright the light. If the light is blue enough, electrons are ejected as soon as the light shines on the metal, and their energy increases as the color of the light moves toward the UV.
It took the genius of Einstein to understand that the experimental observations could be explained if light is a stream of particles, each with the energy given by Planck’s formula E = hf. In this case, a light particle with sufficient energy would be able to knock out an electron from the metal. Einstein thus proposed that each particle of light carries a quantum of energy according to the color of its light. He named the light particles quanta. We now call them photons.
Putting it in terms of light that we can see, red light is composed of individual particles (also called quanta, or photons), where each individual particle (quantum, or photon) has less energy than a particle of violet light.
According to Einstein, red light is composed of low-energy quanta, so no one quantum would be energetic enough to knock electrons out of the electrode from Figure 24a. Increasing the intensity of the light does nothing more than increase the number of light quanta showering on this electrode, all of them too weak in energy to liberate an electron from the metal.
Beyond a certain threshold frequency, the individual light quantum is energetic enough on its own to liberate a single photoelectron. Above this frequency threshold, a change in intensity would change the number of photoelectrons that are released. However, since only one light quantum of sufficient energy is needed to liberate one photoelectron, the photoelectric emission with high-frequency light will happen no matter how weak the intensity of the light.
In 1921, Einstein won the Nobel Prize for his discovery of the law of the photo-electric effect.
From now on, to keep things consistent, we’ll call particles of light by their modern name: photons. This name applies whether we talk about a photon corresponding to the very low frequencies of radio and microwaves, the visible spectrum, or the extremely high frequencies of cosmic gamma rays.
You can experiment with the photoelectric effect using a phototube, such as that shown in Figure 25. The device is a gas-filled or vacuum tube that has an electrode (the photocathode) which expels electrons when illuminated by a light source. The photo-electrons can be collected by a thin wire electrode (the anode), causing a current to flow through a closed circuit. The cathode is typically coated with one or more alkali metals (e.g., lithium, potassium, and cesium). Unlike other metals, which emit photoelectrons only when illuminated by UV light or X-rays, the energy of visible-light photons suffices to release electrons from alkali metals via the photoelectric effect.
Figure 25 The photoelectric effect requires light to act as a stream of particles. (a) Low-frequency photons (red light) do not supply enough energy to eject electrons from the metal cathode of a certain phototube. (b) Blue photons have enough energy to overcome the “work function” of the metal and eject photoelectrons.
For an electron to be ejected from the photocathode, the energy it gains must be greater than some energy Wo necessary for the electron to free itself from the metal. Wo is called the work function and is a property of the metal from which the electrons are to be ejected. Since the energy of a photon is given by E = hf, photoelectrons can be liberated only if E > Wo. A photon with energy equal to Wo is barely able to liberate an electron from the metal. However, if the photon carries more energy than Wo, the electron will be ejected with some kinetic energy.
For example, if the metal plate is made of sodium, which has a work function Wo = 3.296 × 10−19 J, the threshold light frequency for photoelectric emission would be:
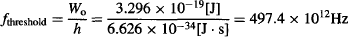
which corresponds to a bright red/orange color. As such, a deep red light will not cause photoelectric emission, showing no current in the microammeter of Figure 25, while blue light will easily cause a photocurrent to flow through the circuit.
Photoelectric tubes were available before the days of semiconductor photodetectors. They were commonly used to read the optical sound tracks of film, and as sensors in burglar alarms and door openers. They are still manufactured for some specific applications (e.g., UV flame detection, spectrophotometers, etc.), but the easiest and cheapest source for these units is the surplus market, for example from Sphere Research in Canada or on eBay. The photocathodes in common phototubes are made with a mixture of alkali metals to make them sensitive over a wide range of wavelengths, usually from IR to UV. To be able to conduct the experiment as shown with red and blue light, you will need to find a phototube with a so-called “S-12” response.
A practical way of experimenting with any available phototube is to place it in a setup similar to that shown in Figure 26. Here, a commonly available RCA 1P39 phototube is illuminated by an LED5. A few inexpensive LEDs of different colors‡ will allow you to collect photoelectric data with photons at different wavelengths. The LED should be positioned so that most of its light falls on the photocathode. Stick a thin (3-mm) strip of black electrician’s tape to the glass envelope of the phototube to shield the anode electrode from direct light from the LED. This reduces the likelihood that spurious photoelectrons from the anode affect your measurements. In addition, you should paint the inside of your enclosure with flat black paint or cover it with matte black tape to prevent reflections from entering the tube.
Figure 26 Build this setup to experiment with the photoelectric effect, (a) A commonly available 1P39 phototube is shown, but many others will work equally well. (b) The phototube and LED should be placed in a light-tight box that is painted flat black on the inside. A thin strip of black electrician’s tape should be used to shadow the phototube’s anode electrode. (c) According to Einstein’s equation for the photoelectric effect, all Vs for various LED frequencies f should fall on a line with slope h/e.
The idea is to use the famous equation developed by Einstein to describe the photoelectric effect:
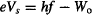
where e = 1.60 × 10−19 Coulomb is the charge of the electron, Vs is the negative voltage that needs to be applied to the anode to stop current from flowing through the circuit (I = 0), Wo is the work function we discussed above (the minimum energy needed to liberate the electron from the photocathode),§ and hf is the energy of the photons striking the photocathode.
By the way, the kinetic energy of an electron accelerated by a voltage V is eV, so Einstein’s equation tells us that the energy necessary to stop the most energetic photo-electron (eVs) equals the energy of the photon that kicks it out of the metal (hf), minus the energy required to liberate the electron from the metal (Wo).
Einstein’s equation predicts that plotting the stopping potential Vs as a function of frequency f should result in a line with slope h/e. If you can’t find the LED’s specs for the exact wavelength of the light emitted, use the values shown in Table 2. Try it out with your apparatus and see how well your data match the equation that won Einstein his Nobel Prize!¶
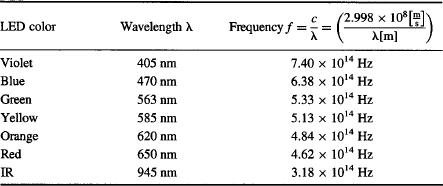
TABLE 2 Wavelengths and Frequencies for the Light Emitted by Some Common LEDs
At what light frequency would you expect Vs to drop down to zero if you extend the line you obtained when graphing your data? This would be the threshold frequency for photoemission for your phototube. You can prove the existence of a threshold by using your IR LED (945 nm). Since the emission from the IR LED is invisible to the human eye you will need to use a digital or video camera (especially one with “night-vision mode”) to verify that your LED is shining bright IR light on the phototube. Close the box and take a reading of photocurrent I with a Vs = 0. Nothing! Nada! Zero! Zip! The LED’s photons at f = 3.18 × 1014 Hz are not energetic enough to kick electrons free from the photocathode.
Another interesting experiment that you should try is to find if varying the intensity of the light has an effect on Vs. Keep the frequency f of the photons constant by using only the green LED. Reduce the intensity of the light by limiting the LED supply current. What do you think will happen?
Lastly, remember that the wave theory predicted that it would take some time for the photocathode to be exposed to light before it starts expelling electrons? Well, you can prove this prediction wrong too by substituting the power supply in the setup of Figure 26 with a fast pulser, and by monitoring the photocurrent with an oscilloscope. This is possible, because unlike incandescent lightbulbs that need to heat up before their light peaks, LEDs turn on as soon as current is applied, and their emission turns off as soon as current is interrupted.
Turning on an LED via a switching device (e.g., a transistor) using its nominal voltage (2.1 V in the case of a green LED) would cause the LED to start emitting photons only after a few microseconds. This is because all of the parasitic capacitances—unintended capacitors that form between the various elements in real-world LEDs and the power supply circuit—need to be charged to the LED’s threshold voltage before light is emitted. To overcome this problem, the circuit of Figure 27a dumps a 2,000-pF capacitor charged to 300 V into the LED, thus causing the LED to produce a pulse of light that starts within 1 ns after the current’s leading edge. The LED will continue to produce light for around 5 μs, as these parasitic capacitances keep on supplying current until they are discharged.
Figure 27 You can measure the time it takes a photoelectric tube to generate a current in response to light. (a) A green LED is turned on very quickly by passing a very brief, very strong pulse of current. At the same time, the photoelectric response is observed with an oscilloscope. (b) Although the response time is greatly slowed down by real-world effects, a nanosecond-level response time is still many orders of magnitude faster than predicted by classical wave theory. (c) Pulsing an LED with a very brief, very strong current causes the circuit to radiate an electromagnetic pulse that couples into the low-level signal line from the phototube, causing a “ringing” artifact that obscures the signal.
When you build the circuit, be careful to keep the wires shown in bold very short. In addition, use thick wires for these connections. Please note that the transistor is not a plain NPN transistor. It is a device designed specifically to work in the “avalanche” mode, which makes it possible to produce very brief, high-power pulses. You must supply the circuit with a minimum voltage of 270 V, which is the avalanche breakdown voltage for the ZTX415 transistor. The trigger pulse is just a >3-V pulse that can be delivered at repetition rates of 100 to 1,000 pulses/min.
As shown in Figure 27c, pulsing an LED with a very brief, very strong current causes the circuit to radiate an electromagnetic pulse that couples into the low-level signal line from the phototube, causing a “ringing” artifact that obscures the signal. For this reason, let’s concentrate instead on the simplified results of Figure 27b, and try to understand what they show. The photocurrent kicks in some 1 ns after current is applied to the LED. How does this 1 ns compare to the predictions of classical wave theory? Go back to the rope bridge analogy of Figure 24b. A wimpy villain would not be able to build enough wave amplitude on that heavy bridge to make you fall before you cross the bridge. He would need as much energy as possible to build up wave amplitude quickly, so he will probably have some of his brutish minions shake the bridge. How quickly you fall off the bridge depends on how fast the brutes are able to transfer energy to the ropes. Energy transfer over a certain period of time is called power. Evil Dr. Wave must surely hope his cronies ate their Wheaties® for breakfast!
Let’s use this analogy to calculate the time it would take a wave to build up enough amplitude in our phototube: let’s suppose that all of the energy in the 2,000 pF capacitor is converted into light by the LED. This is not a realistic assumption due to the inherent losses of the circuit and the LED’s intrinsically low conversion efficiency, but let’s suppose 100% efficiency nevertheless. The optical pulse’s power is thus:
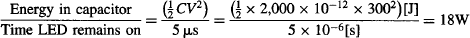
Let’s also assume ideal conditions, and suppose that all of this light could be transferred to build up enough of a wave amplitude to shake electrons from the atoms on the surface of the photocathode. Let’s assume that the atoms in the photocathode are evenly distributed and each takes 1 × 10−19 m2 of the photocathode’s surface area. If the light from the LED illuminates 3 cm2 of photocathode surface, then each atom can absorb energy at a maximum rate of:
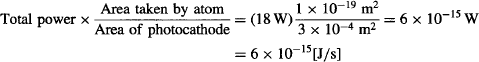
The work function Wo of the photocathode in our tube is 2.24 × 10−19 J, so according to classical wave theory, it would take an electron being supplied at 6 × 10−15 W at least 2.24 × 10−19 J/6 × 10−15 [J/s] = 37.333 μs to escape from the metal under absolutely optimal conditions.
These 37.333 μs are 37,333 times longer than the 1 ns that our real-world experiment showed as a worst-case response time! This factor increases by a few orders of magnitude if you account for the LED’s inefficiencies, turn-on time, and so on. Once again, the wave theory of light is discredited!
Leave a Reply