High school and college physics teachers love to torture their students with something known as the “simple harmonic oscillator.” A good, classical example is a simple mass attached to an idealized spring that oscillates back and forth when given a little tug. The idealized spring is one which doesn’t have any mass itself and does not have any friction or drag of any kind.
Since such a spring always exerts a force proportional to how much it is stretched, it follows that its potential energy increases as the square of the deviation from its natural length, whether it is stretched or compressed. So you can add energy to the system simply by stretching the spring a certain amount and then releasing the mass.
In the ideal case, the resulting motion is called harmonic oscillation, because the mass oscillates back and forth with the same amplitude forever. As it oscillates it constantly converts the energy of motion (kinetic energy) to potential energy and back again. A plot of the position of the mass versus time will look like another sine function.
In addition to a nice example for elementary physics textbooks, this is also a decent approximation for the charged particle oscillations that Max Planck imagined going on in the walls of a heated solid. We already know what his semi-quantum treatment predicted in terms of oscillation energies. Let’s see what comes out of a more complete treatment using Schroedinger’s wave mechanics.
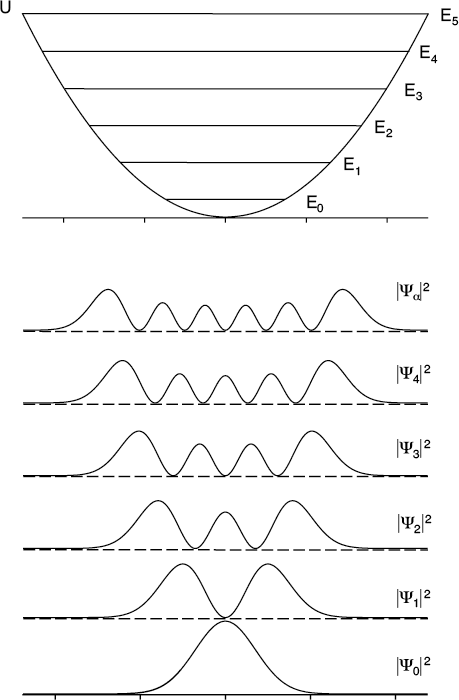
The allowed energies levels of a quantum oscillator are equally spaced, precisely as Max Planck predicted. And, just as the amplitude of a classical oscillator increases as its energy increases, the quantum oscillator spreads further and further beyond the center “equilibrium” position as its energy goes up. Higher energy solutions have more nodes, too.
Let’s start with a plot of the potential energy function, which is just a simple bowl-shaped curve (in one dimension, at least). The center of the curve corresponds to the location of the mass when the spring is neither stretched nor compressed. This is the equilibrium position where the force from the spring would be zero. In either direction from that point, the potential energy increases and so does the force pushing the mass back toward the center.
When we pop this into Schroedinger’s equation and then turn the crank, we again find that only certain values of energy are allowed. Once again, the corresponding wave functions look like standing waves. The situation resembles that of the square wells we studied earlier however in this case the width of the well is also increasing at higher energies. The effect of this is to equalize the spacing of the energy levels. They are equally spaced like rungs in a ladder–exactly as Planck had hypothesized!
It’s also worth noting that a quantum oscillator will spend some time stretched to an extent not permitted by classical physics. The wave function solutions in this case display the same sort of “penetration depth” into the forbidden zones as we saw in the finite square well.
Although we have only looked at this example in one dimension, it does have some real applications. In particular, when two atoms are bound together into one molecule (a “diatomic” molecule) the force that holds them together is approximately like a spring force. A diatomic molecule always has some energy, and some of that energy is in the form of vibrations along an axis connecting the centers of the two atoms. The energy of these vibrations turns out to be quantized just as this model predicts, as long as the vibrational energy is not too great.
Leave a Reply