In the case of a free particle, Schroedinger had little to offer that hadn’t already been understood since de Broglie’s time. To get the real bang for Schroedinger’s buck, we need a more interesting potential energy function. The simplest case would be a region of zero potential energy surrounded by a region of constant but non-zero potential energy. Physics professors and their students refer to this fondly as the old “particle in a box.”
In order to simplify things, we’ll stick to our one dimension, i.e., motion along a single line in one direction that we’ll keep calling x. It may be hard to visualize a box in only one dimension. What we’re really imagining is a force that varies along one dimension in a way that confines the particle to that very region, spanning, say, from x = 0 to x = L. Since the corresponding potential energy function looks like a well, we also call these imaginary things “potential wells.”
As usual, the energy of the particle plays a major role in determining its behavior. If the total energy of the particle is less than the potential energy outside the box, then we say that the particle is confined to the inside of the box.
The analogy with classical mechanics can help us here, as long as we don’t take it too far. Total energy is the sum of potential and kinetic energy. Since the kinetic energy for a real particle can be equal to but not less than zero, the total energy must be equal to or greater than the potential energy. Stated differently, particles can’t exist in any region where the potential energy would be greater than the total energy. Such regions are called classically forbidden regions.
DEFINITION
A classically forbidden region is any region of space in which the potential energy of a particle is greater than its total energy. In classical physics, the particle simply cannot exist in such regions, because there is no such thing as negative kinetic energy.
Let’s first consider the case where the potential energy is infinitely positive in the outer regions. This will guarantee that any particle will stay in the region between the walls. Given the discontinuous nature of the potential energy, the Schroedinger equation is most easily solved by treating the three different zones separately. That is, you solve the equation three times—once when the particle is to the left of the well, once when it’s to the right, and once when it’s confined inside.
Once we have our mathematically allowed solutions, we need to ensure that the solutions match up at the boundaries between the zones. This is an example of the boundary conditions we talked about in the last. The boundary conditions in this case require that the wave functions must be exactly zero at the walls of the box.
Inside the box, the potential energy is zero. This means that the valid solutions are the same as for the free particle in the previous section. But now, not just any energy will do. Only certain energies will correspond to wave functions that equal zero at both boundaries. And, we need combinations of plane waves that are equal parts moving left and right.
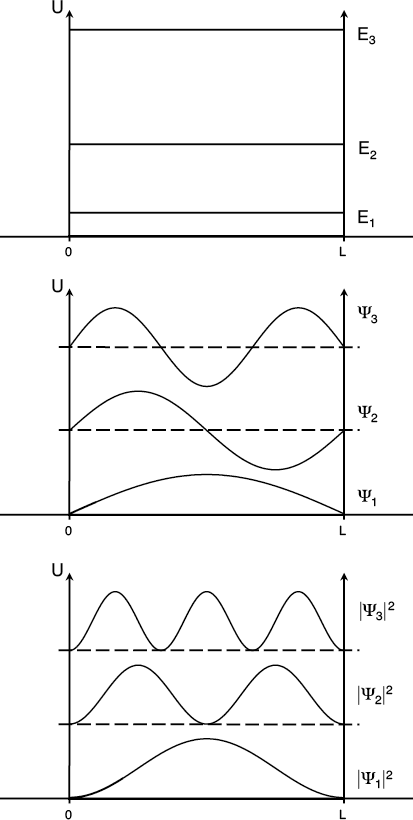
The first three energies (top), wave functions (middle), and probability distributions (bottom) for a particle confined by regions of infinite potential energy.
These solutions are called standing waves because the wave functions behave just like waves on a string that is fixed at both ends (much like the waves we introduced to the Bohr atom). The length of the string corresponds to the width of the potential well in this case. The particle itself is not moving, but its wave function is oscillating at a particular frequency at all locations within the well. These waveforms do not appear to travel at all, since the end points must remain locked at zero at the boundaries.
DEFINITION
Standing waves are patterns of oscillation that do not travel in space. Instead, different locations along the standing wave all oscillate with the same frequency, but the amplitude varies.
Standing wave patterns usually have nodes, which are certain fixed locations where there is no oscillation. This is easiest to visualize when there is only one dimension, but it happens in two and three dimensions as well.
The various solutions have progressively higher energies. The wave functions with higher energy also have higher frequencies (as we have seen before) and thus shorter wavelengths. The allowed energies are not equally spaced, and the energy released if a particle would jump between wave functions gets larger as the energies get larger.
Notice that these standing waves all have a different number of locations where the wave function passes through zero. We call these spots nodes. Besides the nodes at each end of the well, each higher energy solution has one more node than the one below it (starting at zero for the lowest energy solution).
Now instead of infinitely high potential energy outside the well, let’s drop it back down to finite values, the same on the left and the right side of the well. For particles with a total energy much, much less than this potential energy value, the solutions are approximately the same as they were for the infinitely deep well. Particles with energies greater than the potential outside the well, on the other hand, are free particles, for which a whole range of plane wave solutions is possible. But let’s take a closer look at the situation in between—standing wave solutions inside the well at energies below but comparable to the value of the confining potential.
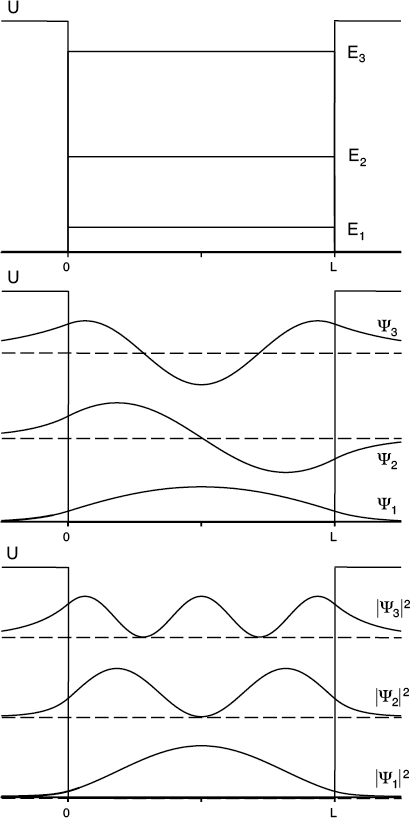
When a particle is confined to a finite quantum box, it leaks ever so slightly into the classically forbidden regions.
Now we see something very interesting. Inside the well, the allowed solutions are still standing waves, each with some number of nodes. But the wave function just outside the well (near the boundaries) is not zero. The wave functions on either side clearly penetrate a little bit into the classically forbidden region before shrinking away to zero. The “amount” of wave function that penetrates depends on the size of the particle’s energy compared to the size of the potential energy that forms the well. In this case, the boundary conditions demand that the full wave functions not only match as you cross the boundary, but that they join up smoothly without any kinks. (In math speak, the value of the wave function and its slope must be continuous at the boundary.)
Leave a Reply