The logarithm

The logarithm arises as the inverse of an exponential function. To further motivate this, let us consider again continuous compounding of interest rates. As we have pointed out, continuous compounding leads to an exponential function that streamlines financial calculations considerably. However, in practice, interest rates are not quoted like this. Typically, interest rates are quoted on an annual basis. Yet, given an annually compounded interest rate r, we could find the equivalent continuously compounded rate r_c and perform calculations based on this rate. Doing so requires solving the equation

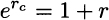
and this in turn requires inverting the exponential function. If we look back at Fig. 2.10 we see that the exponential function f(x) = e^x is a very nice continuous and monotonically increasing function, and therefore it can be inverted over the whole real line. This leads to the definition of the natural logarithm function:

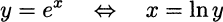
This definition implies that

Plotting the logarithmic function ln x just requires plotting the exponential and swapping the axes, which results in the graph of Fig. 2.15. Natural logarithm is defined only for strictly positive x; it is positive for x > 1, negative for x < 1, and ln 1 = 0. Many years ago tables were provided to carry out calculations with logarithms. Now, logarithms are easily calculated using many software tools, including spreadsheets.

Example 2.14 (A financial example) Say that the annually compounded interest rate is r = 5%. Which continuously compounded rate corresponds to this rate? We have

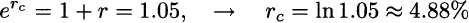
Please note that r_c is smaller than r, because of the effect of continuous compounding on capital growth.

PROPERTY 2.6 Here we summarize a few useful properties of natural logarithm, which are a direct consequence of the properties of exponential function:

• ln(xy) = ln x + ln y
• ln(1/x) = − ln x
• ln(x/y) = ln x − ln y
• ln x^y = y ln x
• ln 1 = 0

Example 2.15 Using logarithms and the properties above, we may finally answer a question we left open: How can we evaluate a^x, when x is an arbitrary real number? This can be accomplished using properties of the exponential:

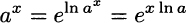
This can actually be calculated, e.g., using expansion (2.6).

Natural logarithms enjoy a privileged status as they are the inverse of the exponential function using base e. If we consider an exponential function with an arbitrary base a, its inverse is base a logarithm:

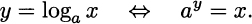
A common case is a = 10, leading to decimal logarithms. The properties that we listed above apply to any logarithm in any base. Incidentally, the notation log_a can be used with any base a. Clearly, ln = log_e, and normally log = log₁₀; however, notation is not always standard, as log is often used to denote natural logarithms.