Under normal conditions, dry, ambient air contains approximately 78.08% nitrogen, 20.94% oxygen, 0.93% argon, 0.04% carbon dioxide, and traces of other gases. For gases, percentages are usually expressed as percent by volume. For an ideal gas (ambient air approximates an ideal gas), volume percent is the same as mole percent. Recall that an ideal gas is one that satisfies the ideal gas law
where
- P = absolute pressure
- V = volume
- n = number of moles
- R = ideal gas law constant
- T = absolute temperature
The units of all terms must be consistent. A common set of units is P in atm, V in liters, n in gmol, and T in degrees Kelvin. For this set of units, R has the value 0.082 06 l‐atm/gmol‐K.
The ideal gas law is very important to air pollution engineers because it is well understood and is quite accurate at normal temperatures and pressures. The ideal gas law can also be written as
where
- M = mass of the sample
- M.W. = molecular weight of the gas
Equations (3.5) and (3.6) can be rearranged to give the mass density of an ideal gas as
Using the set of units mentioned previously, and units of gram per mole for the molecular weight, the density ρ has units of gram per liter.
Note that the NAAQ standards listed in Table 3.9 are given in units of ppm or micrograms per cubic meter (μg/m3). These are common units of concentration measurement in air pollution work, and for gaseous pollutants they are related to each other through the ideal gas law, as will be shown later in this section. First, let us briefly review the meaning of ppm. The concentration measure ppm is simply the mole fraction or volume fraction of the pollutant in the gas mixture multiplied by a factor of 1 000 000; that is,
Note that the denominator in Eq. (3.8) is the total volume of gas and not just the volume of air. The results are similar at low concentrations but are not exactly the same, as shown in the following example problem.
EXAMPLE 3.5
Exactly 500.0 ml of carbon monoxide (CO) is mixed with 999 500 ml of air. Calculate the resulting concentration of CO in ppm.
SOLUTION
Using Eq. (3.8),
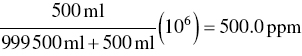
Exactly 500.0 ml of CO is mixed with 1.000 m3 (1 000 000 ml) of air. Calculate the resulting concentration of CO in ppm.
SOLUTION
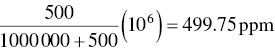
For engineering purposes, the results in Example 3.4 might well be considered identical, but at concentrations ranging upward from a few percent (2.0% = 20 000 ppm), a misunderstanding of the definition will result in significantly wrong answers.
Recall that the two common measures of concentration in air pollution work are ppm and μg/m3. By using the ideal gas law, it is relatively straightforward to convert ppm to μg/m3. However, it is necessary to specify a temperature and a pressure because a gas may occupy different volumes depending on these parameters in air pollution work; the reference conditions are usually chosen as 25 °C and 1.0 atm.
Solving the ideal gas law first for the volume of the pollutant and then for the volume of the total gas and relating the two volumes, we obtain the volume fraction as
where the subscripts p and t indicate pollutant gas and total gas, respectively. Recognizing that np is merely Mp/M·Wp, Eq. (3.9) can be rearranged as
(3.10)
or, substituting for nt,
(3.11)
The mass concentration of pollutant is
With P = 1.0 atm, T = 298 K (25 °C), and R = 0.082 06 l‐atm/gmol‐K, then P/RT has a value of 0.0409 gmol/l, which is the reciprocal of the molar volume of an ideal gas at the stated conditions.
The mass concentration given by Eq. (3.12) has units of g/l which are not the most convenient for reporting pollutant concentrations in air. To obtain the more common units of μg/m3, the left side of Eq. (3.12) must be multiplied by a factor of 109 (the product of 103 l/m3 and 106 μg/g)
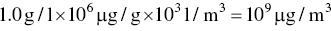
Furthermore, to substitute ppm into Eq. (3.12) for the volume fraction, it is necessary to divide by a factor of (10)6 because ppm is numerically one million times greater than the volume fraction. The net effect is to multiply the right side of Eq. (3.12) by a factor of 1000. Thus, in the form we desire, Eq. (3.12) becomes
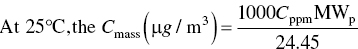
Keep in mind that in the air pollution work, it is typical to define standard temperature as 25 °C (298 K). Where the volume per mole of an ideal gas has the value 22.4 l/mol at T = 0 °C (273 K) and P = 1 atm.
So the final version is
where Cmass = mass concentration (μg/m3) and Cppm = volume concentration (ppm).
EXAMPLE 3.6
(a) What is the AAQS for ozone (eight‐hour averaging time), expressed in μg/m3? (b) The average daily concentration of sulfur dioxide is observed to be 410 μg/m3 at 25 °C and 1 atm in an industrial complex. What is the 24‐hour average concentration of SO2, expressed in ppm?
SOLUTION
- The ozone standard is 0.075 ppm. Using Eq. (3.13),

- The molecular weight of sulfur dioxide is 64.0. Rearranging Eq. (3.13) to solve for the SO2 concentration in ppm, we find that

This concentration of SO2 is above the NAAQ primary standard of 0.14 ppm (based on a 24‐hour average value presented in Table 3.9).
EXAMPLE 3.7
The maximum concentration of dust (particulate matter, PM‐10) in atmosphere during a 24‐hour period was found to be 0.000 128 grain per dry standard cubic foot (gr/dscf). What is the equivalent concentration in μg/m3?
SOLUTION
From Table A.1, it is found that 7000 gr = 454.4 g (1.0 lb) and 1 ft3 = 0.028 33 m3. Hence 1 gr/ft3 equals 2.29 g/m3. Therefore,
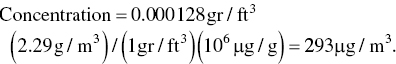
This value is relatively high and exceeds the 24‐hour NAAQ ambient standard of 150 μg/m3 (based on a 24‐hour average value presented in Table 3.9).



Leave a Reply