The EPR Paradox

In 1935, after a lull in the long-running debate between Bohr and Einstein, the latter genius stunned the physics community with another important Gedankenexperiment. Even though Bohr had successfully refuted all of his arguments to date, Einstein was not quite ready to accept the Copenhagen interpretation. He still wasn’t happy with the inherent uncertainty in quantum physics and the loss of determinism. But now he set his sights on the measurement problem and the fundamental issue of objective reality.

QUANTUM QUOTE

Quantum mechanics is very worthy of regard. But an inner voice tells me that this is not yet the real deal. The theory yields much, but it hardly brings us closer to the Old One’s secrets. In any case, I am convinced that He does not play dice.

—Albert Einstein to Max Born, 1926

Shortly after immigrating to the United States, Einstein teamed up with two younger colleagues, Boris Podolsky and Nathan Rosen, to propose what is now known as the EPR paradox (named using the first letters of the authors’ last names). Their objective was to determine whether quantum physics should be considered the complete and correct theory of nature that Bohr, Heisenberg, and Born had claimed it to be at the Solvay Conference in 1927. To do so, they imposed what appeared to be a common sense requirement for such a theory: they reasoned that a proper theory should describe physical quantities that were objectively real. Quantities that only became definite when observed would not qualify.

Recall that in the Copenhagen interpretation, a particle doesn’t have a definite position until and unless its position is measured. At the moment of the measurement, the wave function collapses to one of the many possible positions. In a sense, the actual position of the particle is created by the observer. Since it is not independent of the observer, the position of a particle could not be considered an objectively real quantity. The EPR authors wanted to develop a scenario within quantum physics in which an unmeasured quantity (like a particle’s position) must have objective reality, contrary to the Copenhagen view.

The formalism of the original EPR paper, using position and momentum, is a bit hard to follow without a lot of math. Here we present a scenario, developed by American physicist David Bohm, that illustrates the essence of the EPR paradox a little more simply. Instead of position and momentum, we will use particle spin, particularly the total spin quantum number equal to ¹⁄₂ that we introduced. Recall that with reference to any specific axis in space, a particle with spin ¹⁄₂ may have that spin oriented in only two possible ways, which we called up and down.

The essential feature of the EPR paradox is having two particles that interact briefly and then move apart, so that they can be detected separately. We must also have a physical law that relates a measurable quantity of the two particles (for example, the conservation of angular momentum). An example would be two electrons (which we’ll call e₁ and e₂) created together in a single event such that their total angular momentum must be zero. This requires that one will be spin up and the other spin down, no matter what axis we choose as the reference for the spin direction. (Note the implication that the same axis is used to measure both electron spins.)

After the two electrons are created, they move off in opposite directions. We assume that they encounter no other interactions in flight until they are detected some time later. Electron e₁ flies straight toward a location we’ll call A, while e₂ simultaneously moves in the opposite direction toward a location called B. Electron spin detectors (e.g., Stern-Gerlach magnets) are located at A and B, but they may or may not be turned on and used. A and B can be located at any arbitrary distance from the point where the electrons started, so let’s put them very far apart, say six trillion miles. (This happens to be the distance that light travels in one year, also known as a “light year.”) Now suppose that the electrons travel at 90 percent of the speed of light. This means that it will take about 200 days for each of them to reach their respective detectors.

We know that the two electrons must have opposite spins, but quantum physics does not tell us which one is spin up and which is spin down. So if we only make a measurement of e₁, the result has a 50-50 chance of being up or down. Likewise if we only make a measurement of e₂, there is a 50-50 chance of it being up or down.

The weird part comes if we measure the spins of both e₁ and e₂. Let’s decide to make the measurement of e₁’s spin at A first, then measure e₂’s spin at B one second later (that is, B is just a little farther from the origin than A). There is still a 50-50 chance that e₁ will be spin up or down. However, if the first measurement shows that e₁’s spin is up, then we know with 100 percent certainty that the result of our measurement of e₂ at B will be spin down. Similarly, if e₁ is found to be spin down, then e₂ must be spin up. This is true, remember, because of the conservation of angular momentum.

What makes this weird is that our measurement of e₁ at A has an impact of the measurement of e₂ at B. Let’s make sure we understand this point. Consider things from the point of view of e₂ as it approaches the location B. It has been over 6 months since it was anywhere near e₁. The detector at A and e₁ are trillions of miles away. If no measurement is made at A, then e₂ has an equal chance of being spin up or spin down. However, if a measurement of e₁ is made at A, then e₂ is suddenly forced to be in exactly one spin state or the other (the opposite state of e₁)!

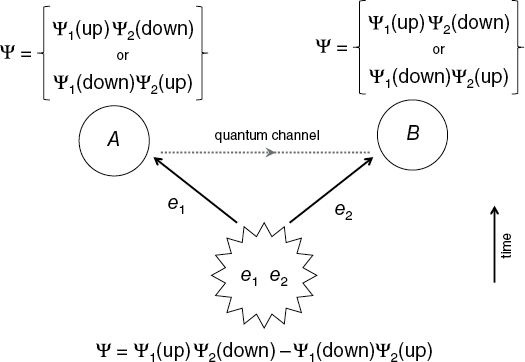
In the EPR Gedankenexperiment, electrons e₁ and e₂ initially share a common origin (bottom). They separate while traveling in space until their spins are measured at points A and B. When e₁ is measured at A, the total wave function collapses, and information is instantaneously transferred to point B though some form of quantum channel. After the measurement, the two electrons are in definite, anti-correlated states. Time in this figure progresses upward.

How could e₂ possibly “know” whether or not e₁’s spin was measured? According to the Copenhagen interpretation, before the measurements both electrons were part of a single, two-particle wave function, flying along as a superposition of equal parts spin up and spin down. Basically, the wave function would look something like this:
Ψ = Ψ₁(up)Ψ₂(down) – Ψ₁(down)Ψ₂(up). When we then make our measurement at location A, we cause the total wave function to collapse into either state Ψ₁(up)Ψ₂(down) or state Ψ₁(down)Ψ₂(up). At that moment, the spin state of each electron is a single and pure quantum state—up or down—and the spins are anticorrelated. Regardless of whether or not we even make the measurement at B, electron e₂ is profoundly influenced by something that happened with electron e₁.