An asset (e.g., a stock share) is sold now at a spot price S0 = $50, where t = 0 is current time. The spot price is the prevailing price at which the asset is exchanged at any moment. The spot price in one year is, of course, uncertain, but say that the expected price in one year is E[S1] = $60. A type of contract that is commonly traded on many assets is a forward contract.20 This contract is signed between two parties who agree on exchanging the asset at some future time (say, one year) for a price that is agreed on now. This fixed price, that we denote by F0, is the forward price at time t = 0. In one year, one of the two parties will sell the item to the other one at price F0, no matter what spot price S1 will prevail in one year. The party agreeing to buy is said to hold the long position; the party agreeing to sell is said to hold the short position. Depending on the relationship between the agreed-on forward price F0 and the future spot price S1, one of the two parties will turn out to be happy, at the expense of the counterpart. If it turns out that S1 > F0, the long position will benefit since she can buy at a price lower than the current spot price. The short position will benefit if S1 < F0, since she can sell at a higher price. A priori, there are different reasons for trading such contracts. One reason is hedging risks away: By fixing the price for the future, long and short parties eliminate risk ex ante. Ex post, one of them will regret the hedging decision, but risk management strategies should be evaluated before uncertainty is resolved. Another reason could be speculation of traders having firm beliefs about future spot prices and willing to bet on their forecasts.
Now the problem is: What should F0 be? Actually, it is the balance between demand and offer that determines prices; still, there are many reasons why one should be interested in finding a sensible estimate of a fair price. One possible guess is that a fair price should be E[S1] = $60. Note that money and the underlying asset are exchanged in the future, so we do not need to discount cash flows, as the forward price F0 will be paid in one year. We have seen before that using expected values to value assets or lotteries ignores risk aversion. Taking this into account, one could argue that the price should be a bit less than $60. But how much less? There are many actors in the markets; whose risk aversion matters most? It seems that there is no hope to find a sensible forward price! By the way, each actor might have a different view of the future, as well as different information, but to keep it simple, let us assume that everyone agrees on the above expectation about S1.
To get some clue, let us assume that the forward price is set as the expected future (spot) price, F0 = E[S1] = $60. Also assume that we may lend or borrow money at an annual risk-free rate of 10%. In this setting, you could adopt the following trading strategy: Borrow $50 now, buy the asset, and enter a short position in the forward (i.e., you agree to sell the asset at the forward price in the future, no matter what the spot price will be). This trade is costless at time t = 0, since cash flows cancel each other and (in principle) no money is needed to enter a forward contract. In one year, you will pay back $55 to the guy who loaned you that money but, whatever the spot price, you will be able to sell the asset for $60, earning $5 for sure. If this were the case, we would have found the perfect money-making machine. Please note that you make money without taking chances and without any need for initial cash, as the initial net cash flow is zero. If you enter a long position at F0 = $60 and the spot price turns out to be S1 = $100, you will make $40 by using the forward contract to buy the asset at $60 and selling it immediately on the spot market. This is much better than the $5 you could make by the riskless strategy, but in doing so, you are taking chances, as the spot price could be well below the forward price and you would lose money. A riskless trading strategy that does not require any money is an example of an arbitrage opportunity.
Could we scale the investment up and make an arbitrary amount of money out of nothing?
Now, remember that you are not alone. If such an arbitrage opportunity were available, many other investors would follow your pattern and buy the underlying asset; this would increase the spot price (not to mention the fact that many people would borrow money, which would affect the interest rate). What could happen is not quite clear, as it depends on complex market dynamics, but we can conclude that those three numbers (spot price $50, forward price $60, risk-free interest rate 10%) are not consistent; they cannot be equilibrium prices and rates.
So, we know that $60 is too high a forward price. It is easy to see that any price higher than $55 leads to a similar arbitrage opportunity. On the other hand, assume that F0 is smaller than $55, say, $52. In this case, you could reverse the trade by selling the asset short (see Example 1.3 on short selling). You borrow the asset, sell it at the current spot price S0 = 50, invest the proceeds at the risk-free rate, and enter a long position in the forward contract. This long position comes in handy, as you will have to give the asset back to the lender in one year. You will do so at the given forward price, $52, after collecting the money you lent plus interest, which is now $55; then, you made $3 for free. A similar strategy can be applied for any forward price less than $55.
The conclusion is that the only arbitrage free forward price is $55. Generalizing a bit, what we found is that, in order to rule out arbitrage opportunities, the forward price should be
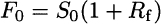
which is a somewhat stunning conclusion: uncertainty does not play any role, as it is the risk-free interest rate Rf that determines the forward price. This conclusion should be taken with care, as it is at odds, e.g., with what we read on newspapers about speculation with futures on oil prices. In fact, the reasoning assumes somewhat idealized financial markets, and it can be more or less justified, depending on the actual asset we are dealing with. While a financial asset can be practically stored at no cost, oil cannot; by the same token, selling oil short is certainly not that easy. Pricing forward and futures contracts is affected by many issues such as transaction costs, differences between lending and borrowing rates, etc. Still, there is an important lesson here:
Uncertainty is important in decision making, but collective behavior may have some surprising effects on it.
Leave a Reply