The success of Bohr’s atom depended on the notion that certain orbits were special, and when electrons occupied these they refrained from radiating away. Physicists were eventually persuaded to buy this, but only because it allowed them to predict the frequency of atomic spectral lines and many other observed atomic phenomenon. Stationary states could not (yet) be explained in terms of anything more fundamental. However, an intriguing concept soon emerged that actually made some headway in this regard. The only problem, though, was that it couldn’t possibly be true.
Suppose that instead of traveling around the nucleus in a circle, such that it was always the same distance from the center, an electron slowly undulated inward and outward as it orbited. Its orbital path would appear as a wavy trajectory superimposed onto the circular orbit. If the wavelength of the oscillation were just the right length, every orbit would trace the exact same path as its previous orbit. In other words, the wavy orbits would join up seamlessly as the electron moved from one revolution to the next.
If for some reason electrons traveled not in perfectly circular orbits but in waves that wrapped around the atom, certain wavelengths would only be allowed at certain distances from the nucleus. Could this have anything to do with the mysteriously stable stationary states?
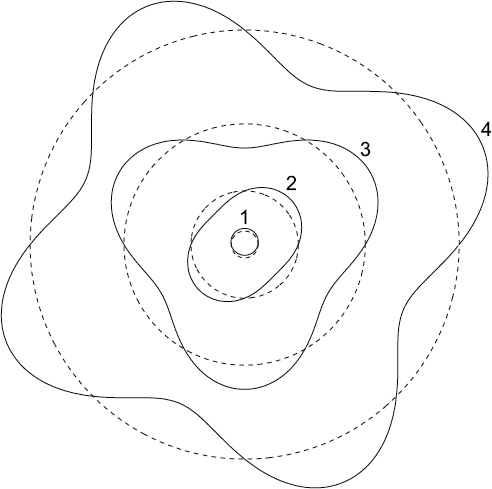
In this representation of the atom, the dashed circles are the first four orbital radii permitted in the Bohr atom, while the solid lines are standing waves superimposed on the allowed Bohr orbits.
When the wavy orbits join up seamlessly in this way, physicists call the result a standing wave. This is because of its similarity to the type of vibration that forms, for example, when a violin string is plucked. Moreover, classical physics tells us that standing waves have an inherent stability and will stick around as long as there is no friction to drain the vibrational energy away.
For an electron that traces a wave while completing its orbit, a stable standing wave would be formed whenever a whole-number multiple of its wavelengths fit nicely into the length (i.e., circumference) of its orbit. If for some reason the electron behaved like a wave with a pre-defined wavelength, then it could form a standing wave only for very specific orbits about the nucleus. Perhaps this could help explain why certain orbits about a nucleus are special?
This would certainly be an elegant way of explaining the privileged nature of stationary states. Alas, if only it could be true. It can’t, of course, because such behavior would only have meaning if an electron exhibited wavelike properties in the first place. But an electron, after all, is a particle. And as a particle, it couldn’t possible behave like a wave. Or could it?
Leave a Reply