THE CLAUSIUS INEQUALITY

The Clausius inequality is given by the equation

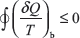
where δQ represents the heat transfer at a part of the system boundary during a portion of the cycle, and T is the absolute temperature at that part of the boundary. The symbol δ is used to distinguish the differentials of non-properties, such as heat and work, from the differentials of properties, written with the symbol δ. The subscript b indicates that the integrand is evaluated at the boundary of the system executing the cycle. The symbol indicates that the integral is to be performed over all parts of the boundary and over the entire cycle. The Clausius inequality can be demonstrated using the Kelvin–Planck statement of the second law, and the significance of the inequality is the same: the equality applies when there are no internal irreversibilities as the system executes the cycle, and the inequality applies when internal irreversibilities are present.

The Clausius inequality can be expressed alternatively as

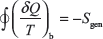
where S_gen can be viewed as representing the strength of the inequality. The value of S_gen is positive when internal irreversibilities are there and zero when no internal irreversibilities are there; S_gen cannot be negative. Thus, S_gen is a measure of the irreversibilities within the system executing the cycle.