Reservoir flow systems are usually classed according to (1) the compressibility of fluid, (2) the geometry of the reservoir or portion thereof, and (3) the relative rate at which the flow approaches a steady-state condition following a disturbance.
For most engineering purposes, the reservoir fluid may be classed as (1) incompressible, (2) slightly compressible, or (3) compressible. The concept of the incompressible fluid, the volume of which does not change with pressure, simplifies the derivation and the final form of many equations. However, the engineer should realize that there are no truly incompressible fluids.
A slightly compressible fluid, which is the description of nearly all liquids, is sometimes defined as one whose volume change with pressure is quite small and expressible by the equation

where
R = reference conditions
The exponential term in Eq. (8.2) can be expanded and approximated, due to the typically small value of c(pR – p), to yield the following:

A compressible fluid is one in which the volume has a strong dependence on pressure. All gases are in this category. In Chapter 2, the real gas law was used to describe how gas volumes vary with pressure:

Unlike the case of the slightly compressible fluids, the gas isothermal compressibility, cg, cannot be treated as a constant with varying pressure. In fact, the following expression for cg was developed:

Although fluids are typed mainly by their compressibilities, in addition, there may be single phase or multiphase flow. Many systems are only gas, oil, or water, and most of the remainder are either gas-oil or oil-water systems. For the purposes of this chapter, discussion is restricted to cases where there is only a single phase flowing.
The two geometries of greatest practical interest are those that give rise to linear and radial flow. In linear flow, as shown in Fig. 8.2, the flow lines are parallel and the cross section exposed to flow is constant. In radial flow, the flow lines are straight and converge in two dimensions toward a common center (i.e., a well or cylinder). The cross section exposed to flow decreases as the center is approached. Occasionally, spherical flow is of interest, in which the flow lines are straight and converge toward a common center (point) in three dimensions. Although the actual paths of the fluid particles in rocks are irregular due to the shape of the pore spaces, the overall or average paths may be represented as straight lines in linear, radial, or spherical flow.
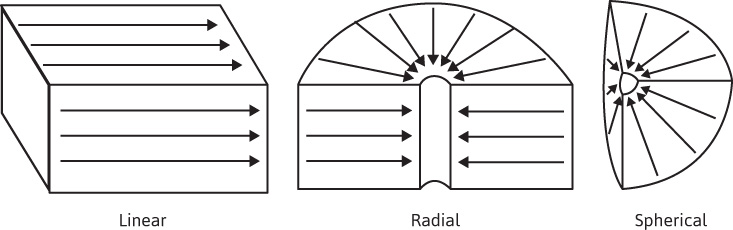
Figure 8.2 Common flow geometries.
Actually, none of these geometries is found precisely in petroleum reservoirs, but for many engineering purposes, the actual geometry may often be closely represented by one of these idealizations. In some types of reservoir studies (i.e., waterflooding and gas cycling), these idealizations are inadequate, and more sophisticated models are commonly used in their stead.
Flow systems in reservoir rocks are classified, according to their time dependence, as steady state, transient, late transient, or pseudosteady state. During the life of a well or reservoir, the type of system can change several times, which suggests that it is critical to know as much about the flow system as possible in order to use the appropriate model to describe the relationship between the pressure and the flow rate. In steady-state systems, the pressure and fluid saturations at every point throughout the system do not change. An approximation to the steady-state condition occurs when any production from a reservoir is replaced with an equal mass of fluid from some external source. In Chapter 9, a case of water influx is considered that comes close to meeting this requirement, but in general, there are very few systems that can be assumed to have steady-state conditions.
To consider the remaining three classifications of time dependence, changes in pressure are discussed that occur when a step change in the flow rate of a well located in the center of a reservoir, as illustrated in Fig. 8.3, causes a pressure disturbance in the reservoir. The discussion assumes the following: (1) the flow system is made up of a reservoir of constant thickness and rock properties, (2) the radius of the circular reservoir is re, and (3) the flow rate is constant before and after the rate change. As the flow rate is changed at the well, the movement of pressure begins to occur away from the well. The movement of pressure is a diffusion phenomenon and is modeled by the diffusivity equation (see section 8.5). The pressure moves at a rate proportional to the formation diffusivity, η,

where k is the effective permeability of the flowing phase, φ is the total effective porosity, μ is the fluid viscosity of the flowing phase, and ct is the total compressibility. The total compressibility is obtained by weighting the compressibility of each phase by its saturation and adding the formation compressibility, or

The formation compressibility, cf, should be expressed as the change in pore volume per unit pore volume per psi. During the time the pressure is traveling at this rate, the flow state is said to be transient. While the pressure is in this transient region, the outer boundary of the reservoir has no influence on the pressure movement, and the reservoir acts as if it were infinite in size.
The late transient region is the period after the pressure has reached the outer boundary of the reservoir and before the pressure behavior has had time to stabilize in the reservoir. In this region, the pressure no longer travels at a rate proportional to η. It is very difficult to describe the pressure behavior during this period.
The fourth period, the pseudosteady state, is the period after the pressure behavior has stabilized in the reservoir. During this period, the pressure at every point throughout the reservoir is changing at a constant rate and as a linear function of time. This period is often incorrectly referred to as the steady-state period.
An estimation for the time when a flow system of the type shown in Fig. 8.3 reaches pseudosteady state can be made from the following equation:

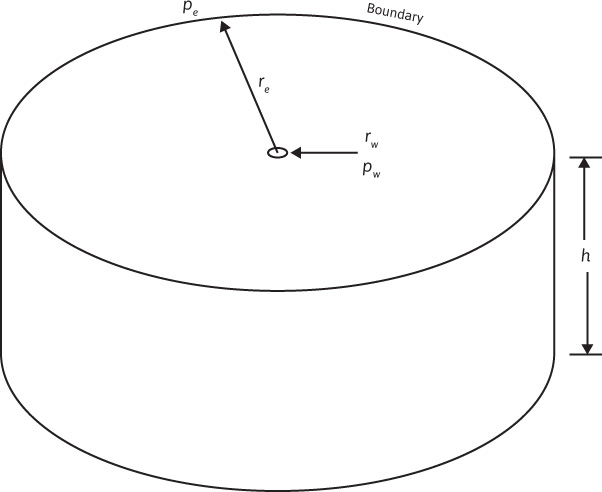
Figure 8.3 Schematic of a single well in a circular reservoir.
where tpss is the time to reach the pseudosteady state, expressed in hours.3 For a well producing an oil with a reservoir viscosity of 1.5 cp and a total compressibility of 15 × 10–6 psi–1, from a circular reservoir of 1000-ft radius with a permeability of 100 md and a total effective porosity of 20%:
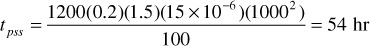
This means that approximately 54 hours, or 2.25 days, is required for the flow in this reservoir to reach pseudosteady-state conditions after a well located in its center is opened to flow or following a change in the well flow rate. It also means that if the well is shut in, it will take approximately this time for the pressure to equalize throughout the drainage area of the well, so that the measured subsurface pressure equals the average drainage area pressure of the well.
This same criterion may be applied approximately to gas reservoirs but with less certainty because the gas is more compressible. For a gas viscosity of 0.015 cp and a compressibility of 400 × 10–6 psi–1,
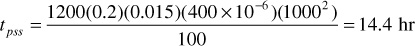
Thus, under somewhat comparable conditions (i.e., the same re and k), gas reservoirs reach pseudosteady-state conditions more rapidly than oil reservoirs. This is due to the much lower viscosity of gases, which more than offsets the increase in fluid compressibility. On the other hand, gas wells are usually drilled on wider spacings so that the value of re generally is larger for gas wells than for oil wells, thus increasing the time required to reach the pseudosteady state. Many gas reservoirs, such as those found in the overthrust belt, are sands of low permeability. Using an re value of 2500 ft and a permeability of 1 md, which would represent a tight gas sand, then the following value for tpss is calculated:
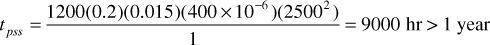
The calculations suggest that reaching pseudosteady-state conditions in a typical tight gas reservoir takes a very long time compared to a typical oil reservoir. In general, pseudosteady-state mechanics suffice when the time required to reach pseudosteady state is short compared with the time between substantial changes in the flow rate or, in the case of reservoirs, with the total producing life of the reservoir. Many wells are not produced at a constant rate, and instead, the flowing pressure may be approximately constant. For such wells during the transient flow condition, the pressure disturbance still moves at the same velocity, and at the time of pseudosteady state, the well reaches a boundary-dominated condition.
Leave a Reply