The efficiency of a heat engine cycle greatly depends on how the individual processes are executed. The net work can be maximized by using reversible processes. The best known reversible cycle is the Carnot cycle.
Note that the reversible cycles cannot be achieved in practice because of irreversibilities associated with real processes. But, the reversible cycles provide upper limits on the performance of real cycles.
Consider a gas in a cylinder–piston (closed system). The Carnot cycle has four processes as (Figure 1.15):
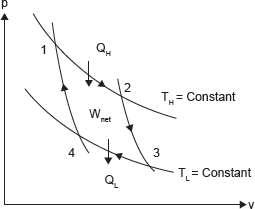
Figure 1.15 P–V Diagram of Carnot Cycle
1–2 Reversible Isothermal Expansion: The gas expands slowly; heat is added reversibly at constant temperature (TH) to the system. Work is done on the surrounding.
2–3 Reversible Adiabatic Expansion: The cylinder–piston is now insulated (adiabatic) and gas continues to expand reversibly (slowly). So, the gas is doing work on the surroundings, and as a result of expansion the gas temperature reduces from TH to TL.
3–4 Reversible Isothermal Compression: The gas is allowed to exchange heat with a sink at temperature TL as the gas is being slowly compressed. So, the surrounding is doing work (reversibly) on the system, and heat is transferred from the system to the surroundings (reversibly) such that the gas temperature remains constant at TL.
4–1 Reversible Adiabatic Compression: The gas temperature is increasing from TL to TH as a result of compression. Carnot cycle is the most efficient cycle operating between two specified temperature limits.
The efficiency of all reversible heat engines operating between the two same reservoirs is the same. The thermal efficiency of a heat engine (reversible or irreversible) is
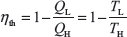
The efficiency of an irreversible (real) cycle is always less than the efficiency of the Carnot cycle operating between the same two reservoirs.

Leave a Reply