TESTING BELL’S INEQUALITY

In 1982, French physicist Alain Aspect was able to run the first experimental test of Bell’s Inequality.⁵⁰ Aspect used a very complex entangled source in which calcium atoms (in an atomic jet) are pumped by a two separate lasers.⁵¹ Using the CHSH form of Bell’s Inequality, Aspect was looking for the value of a certain coincidence statistical parameter (S) to be equal or lower than two if local hidden variables are present. On the other hand, quantum mechanics predicted S = 2.7. Aspect’s experimental result was S = 2.697 ± 0.015, providing overwhelming support to the thesis that Bell’s Inequality is violated in its CHSH version, thus confirming quantum indeterminacy.

Figure 147 and Figure 148 show how you can use the entangled-photon source that uses two BBO crystals (Figure 142) and SPAD-based SPCMs (Figure 144) to conduct a modern replication of Aspect’s experiment. The general idea is to count photons detected by two SPCMs, as well as their coincidence counts^‡‡ for the set of angles for the polarizers that precede the SPCMs, as shown in Table 10.

Figure 147 This setup uses the entangled-photon source of Figure 142 to test the CHSH version of Bell’s Inequality. The coincidence detection circuit is shown in Figure 144. (a) In its simplest form, photons are filtered and focused directly onto the SPADs. (b) We use Perkin-Elmer SPCMs with fiber-optic connector inputs, which allow us to route photons from small, light collection heads to the SPCMs placed outside the optical breadboard.

Figure 148 Our entangled-photon setup is enclosed within a light-tight box made of black foam board. The laser, BBO crystal, and aluminum arms holding the fiber-optic collectors fit on an 18-in. × 18-in. bench plate. Fiber-optic jumpers convey photons to three surplus Perkin-Elmer SPCMs that we purchased on eBay.

TABLE 10 Photon Counts and Coincidence Counts you should Acquire for these Polarization Settings for the Polarizers Preceding the SPCMs of Figure 147

Case	Polarization angle α for polarizer preceding SPCM “A”	Polarization angle β for polarizer preceding SPCM “B”
1	-45°	-22.5°
2	-45°	22.5°
3	-45°	67.5°
4	-45°	112.5°
5	0°	-22.5°
6	0°	22.5°
7	0°	67.5°
8	0°	112.5°
9	45°	-22.5°
10	45°	22.5°
11	45°	67.5°
12	45°	112.5°
13	90°	-22.5°
14	90°	22.5°
15	90°	67.5°
16	90°	112.5°

Please note that the detectors are very sensitive to photons at the UV pump wavelength. The 780-nm long-pass filters drastically reduce the number of UV photons that make it through, but the UV photons would far exceed the number of entangled photons if shading were not used. We constructed the combined beam stop/collimator of Figure 149 to absorb pump photons that go through the BBO crystals, as well as to allow only photons in the ± 3° beams to pass through to the detecors. If required, you may install an IR long-pass filter (e.g., Thorlabs FGL15S or a photographic R-72 filter) behind the collimation holes to further reduce UV photon leakage. Another trick that works well is to place the laser relatively far away from the BBO crystals (you may bend the path around with UV-enhanced aluminum mirrors if necessary) such that the laser’s spot at the beam stop is small, and does not overlap with the ± 3° entangled-photon beams.

Figure 149 Many UV photons can go through the 780-nm long-pass filters preceding the detectors, so we constructed this beam stop to shade the detectors from photons that don’t belong to the entangled beams at ±3°. The foam board is simply hot-glued to two ¹/₄-in. T-nuts positioned on a ¹/₄-in. 20-threaded rod. This beam stop is screwed on the breadboard 12 in. away from the BBO crystals.

Before taking measurements to test Bell’s Inequality, your setup will need to be aligned^§§ to yield the highest count of entangled photons on the coincidence channel when the polarizers in front of the SPCMs are set to the same polarization angle (α = β). This requires an enormous amount of patience. It is best accomplished by first aligning the major mechanical components (without the IR filters) using a visible laser projected “backward”—that is, starting from the position that the SPCMs will occupy, and then toward the plane where the BBO crystals will lie (we substitute the BBO crystals by a 1-in.-OD × ¹/₄-in.-ID steel washer). We use a red laser pointer that we focus onto a Thorlabs F220FC-B fiber coupler as a laser source for this step. We can therefore project a laser from the position of the photon-collection heads (Figure 147b) by injecting the laser into the fiber-optic patch cords. Next, we place a mirror within the BBO crystal holder and further refine the alignment by checking that the reflection of the laser projected from one of the photon-collection assemblies reaches the other photon collector. At this point, we place the BBO crystal and IR filters in place, substitute the red laser with an IR unit (30 mW, 980 nm; Information Unlimited model LM980-30), and tweak everything again before connecting the fiber-optic patch cords to the SPCMs.

Next, we align the 405-nm pump laser. This laser should be rotated to maximize the intensity of the beam going through the 45° glass polarizer placed before the BBO crystals. The next step is to find the best angle for the SPCMs. Turn off all lights and turn on the SPCMs. Turn on the pump laser and move one of the SPCMs around 3° ± 1° to find the angle that produces the most counts. Set the second SPCM to the same angle. Next, ensuring that α = β = 0°, move the SPCMs very lightly to maximize the number of coincidence counts. Depending on your laser’s power, the number of coincidence counts should be in the range of 300–1,000 counts per second when the irises on the SPCMs are fully opened. Next, adjust the quartz -wave waveplate to maximize the number of individual and coincidence counts. Then, change the polarizing angles α = β = 45°, and tweak the pump laser’s polarization so the coincidence counts obtained at α = β = 45° are as close as possible to those at α = β = 0°. Lastly, substitute a 1-in.-OD × -in.-ID steel washer for the BBO crystal assembly temporarily, turn on the pump laser, and obtain channel and coincidence-count background for your system at all angle settings (all angles shown in Table 10). You will need to subtract these background counts from your raw data to estimate the number of events caused by entangled IR photons. We must stress again that the alignment process is very tedious and demands great patience!

We are finally ready to collect actual data at the polarization angles given in Table 10. Run the acquisition until you get at least 1,000 coincidence counts (after subtracting background counts) for the (α = -45°, β = -22.5°) setting. The exact amount of time is not important, but the same acquisition time should be used for all settings.

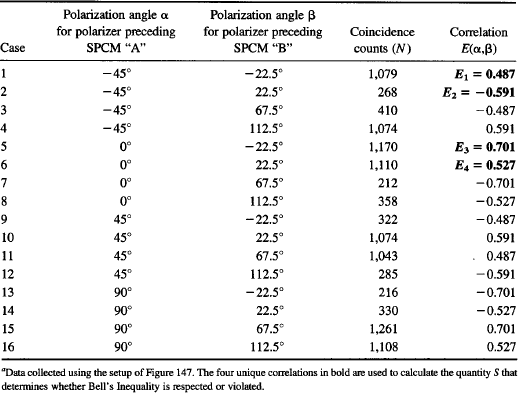
Testing the CHSH version of Bell’s Inequality involves calculating the correlations between coincidence counts at the various angle settings. Please take a look at Table 11, where the correlations are calculated for the 16 cases using our setup:

TABLE 11 Coincidence Counts and Calculation of Correlations to Test the CHSH Version of Bell’s Inequality^a

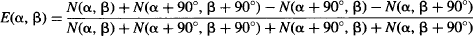
For example, E for case 1 is calculated:

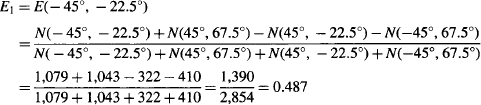
As you can see from Table 11, there are really only four unique correlations for this set of 16 angle combinations. We have bolded them on the table. The first is the one that we just calculated. The other three are:

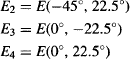
Let’s skip over the derivation⁵² of the CHSH form^¶¶ of the Bell Inequality for our setup, and jump straight to the inequality we need to test. The quantity to calculate is:

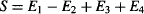
where |S| ≤ 2 if local hidden variables exist, and S > 2 if the Copenhagen Interpretation is correct.^{|| ||} For the experimental data in Table 11, S = 2.305, which is a clear violation of the Bell Inequality!