Let’s revisit the original particle-in-a-box problem (Figure 109). We had assumed that the system had a specific energy that did not vary with time. This allowed us to use a simple form of Schrödinger’s equation that gave us the wavefunctions of the system that depend only on the position x within the box, and the system’s quantum number n:
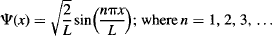
We then took some quantum dots and illuminated them with UV light (Figure 112) to take them from their ground state (n = 1) to their first excited state (n = 2). The quantum dots spend some time in the excited state, but eventually return to their ground state by emitting a photon with a wavelength dependent on the radius of the quantum dot.
Since there are a huge number of quantum dots in each vial, some dots are in the ground state ready to absorb UV light, while some are in the excited state ready to decay back to the ground state by emitting a photon. As long as we don’t try to observe a quantum dot, all we can know is the probability that it may be in the ground or excited states. However, we saw that each of these states has a different wavefunction, so the wavefunction for the quantum dot exposed to UV light is really shifting between these two wavefunctions. The combined wavefunction is the superposition of the two static wavefunctions, and it now varies as a function of time. The time-dependent Schrödinger equation is more difficult to solve, but you should be able to see how it behaves in Figure 118. The probability function is now a blend or superposition of the individual wavefunctions for the system’s ground state and first excited state. The probability of finding the particle at a certain position x within the box now also depends on when the box is observed. When the box is not observed, the probability function moves back and forth with time. The physical interpretation of the wavefunction would be that the system is in a superposition of both states until observed. That is, the particle is both at the ground state and in the excited state until observed, at which time the particle may be found at a certain position with probabilities given by the time-dependent Schrödinger equation.
Figure 118 A particle in a box that oscillates between its ground state and first excited state has a wavefunction in which the wavefunctions of each state are superimposed and vary with time. In contrast to a particle in a box at a single quantum state, the probability of finding the particle at a certain position x within the box now also depends on when the box is observed. When the box is not observed, the probability function moves back and forth as time progresses.
Now, Schrödinger was not the one who interpreted the wavefunction as a wave of probability. He, along with Einstein, absolutely hated the idea that a system would really be in a superposition of states until observed. In opposition to Bohr’s group in Copenhagen, Schrödinger and Einstein believed that a particle is in a definite state before we observe it, and the fact that quantum mechanics could only provide an answer in terms of probability meant the theory was incomplete. They were convinced that Determinism would rise triumphant once quantum physics was developed to the point where it could predict the precise state of a system, not only the probability of finding a system in a certain state. In contrast, the Copenhagen Interpretation explains that the system undergoes collapse into a definite state only when the system is measured.
Einstein wrote a letter to Schrödinger comparing the superposition of states in a quantum system to the state of an unstable keg of gunpowder that, under the Copenhagen Interpretation, will contain a superposition of both exploded and unexploded states. Schrödinger took this idea to its extreme in his famous thought experiment, attempting to disprove it by stating its absurd consequences. In Schrödinger’s words:
One can even set up quite ridiculous cases. A cat is penned up in a steel chamber, along with the following device (which must be secured against direct interference by the cat): in a Geiger counter, there is a tiny bit of radioactive substance, so small that perhaps in the course of the hour, one of the atoms decays, but also, with equal probability, perhaps none; if it happens, the counter tube discharges, and through a relay releases a hammer that shatters a small flask of hydrocyanic acid. If one has left this entire system to itself for an hour, one would say that the cat still lives if meanwhile no atom has decayed. The wavefunction of the entire system would express this by having in it the living and dead cat (pardon the expression) mixed or smeared out in equal parts.
Since you already know about wavefunctions, we will modify Schrödinger’s experiment by tagging the cat’s left ear, as shown in Figure 119. This will let us represent the state of the cat by the ear’s position along the x axis. If the cat is alive, it will sit and its ear will be at x = l. If the cat is dead, then the ear’s position will be x = d.
Figure 119 In our version of Schrödinger’s cat thought experiment, we tagged the cat’s left ear so we can represent the cat’s state by the ear’s position along the x axis (either at l for live or at d for dead). The cat is definitely alive before we start the experiment at t = 0, so the position of the ear is x = l. The box is then closed, and Schrödinger’s experiment is allowed to proceed, placing both states into superposition. After 1 hour there is exactly 50%/50% probability that the poison did or did not kill the cat, so |Ψ|2 evenly distributes the probability of finding the ear tag at x = l or x = d. Once the box is opened, the wavefunction collapses into a certain position at either x = l or x = d.
Before this diabolical mechanism is turned on, the cat is definitely alive, so there is absolute certainty that the position of the ear is at x = l. The box is then closed, allowing the mechanism to start working. Just as in Schrödinger’s original experiment, a radioactive substance inside the box has exactly 50%/50% chance of undergoing one radioactive decay in one hour. Poison is released inside the box if a Geiger counter detects radioactive decay, so the probability of finding the ear tag at x = l decreases as time progresses, while at the same time, the probability of finding it at x = d increases. The wavefunction for the ear’s position is thus a superposition of the wavefuction for the cat’s state, in which x = l (cat is alive), and the cat’s state in which x = d (cat is dead).
The wavefunction would slowly evolve from having a single peak at x = l (cat is definitely alive at t = 0), to having peaks of equal height at x l and x = d (cat is in superposition of states) at the 1-hour mark, when there is exactly 50%/50% chance of the poison having been released. Do you see the similarity between the way in which the cat’s ear position wavefunction changes with time and the plots of Figure 118? Figure 118a would correspond to some early time during the experiment, when there is very high probability of finding the cat alive. As time progresses, the probability of finding it alive decreases, while the probability of finding it dead increases, until the wavefunction gets to Figure 118h, in which there is the same probability of finding it dead or alive. Past 1 hour, the probability of finding the cat dead is higher than finding it alive, until the wavefunction of Figure 118i is reached, when there is almost no chance of finding a live cat.
Schrödinger meant this example to be a criticism of the Copenhagen Interpretation of the wavefunction, which implies that the cat remains both alive and dead (to the universe outside the box) until the box is opened. That is, when asked whether the cat is dead or alive during the hour of waiting, the Copenhagen Interpretation would answer that the cat is in a superposition of dead and alive until you look in the box. Then, and only then, does the act of measurement (looking in the box) “collapse the wavefunction,” resulting in a cat that’s definitely alive or dead.
Einstein and Schrödinger simply could not accept that reality is suspended when it is not being observed. This thought experiment really highlights the main philosophical issues that result from quantum mechanics, including the meaning of the quantum waves, the process of measurement, and the involvement of measuring instruments and observers in processes being studied.
Today, physicists no longer find the process mysterious and intractable, mostly because no physical meaning is given to the wavefunction. Instead, Ψ is understood to be just an abstract mathematical function that contains statistical information about possible experimental outcomes. Whenever the quantum system is measured, the mathematical form of Ψ simply changes, which is common behavior for an abstract mathematical representation, and which doesn’t cause any philosophical problems.
Leave a Reply