We took a rather standard view. On the one hand, we have introduced events and probabilities according to an axiomatic approach. On the other hand, when dealing with inferential statistics, we have followed the orthodox approach: Parameters are unknown numbers, that we try to estimate by squeezing information out of a random sample, in the form of point estimators and confidence intervals. Since parameters are numbers, when given a specific confidence interval, we cannot say that the true parameter is contained there with a given probability; this statement would make no sense, since we are comparing only known and unknown numbers, but no random variable is involved. So, there is no such a thing as “probabilistic knowledge” about parameters, and data are the only source of information; any other knowledge, objective or subjective, is disregarded. The following example illustrates the potential difficulties induced by this view.24
Example 14.13 Let X be a uniformly distributed random variable, and let us assume that we do not know where the support of this distribution is located, but we know that its width is 1. Then, X ∼ U[μ−0.5, μ+0.5], where μ is the unknown expected value of X, as well as the midpoint of the support. To estimate μ we take a sample of n = 2 independent realizations X1 and X2 of the random variable. Now consider the order statistics

and the confidence interval

What is the confidence level of I, i.e., the probability P{μ ∈ I}? Both observations have a probability 0.5 of falling to the left or to the right of μ. The confidence interval will not contain μ if both fall on the same half of the support. Then, since X1 and X2 are independent, we have
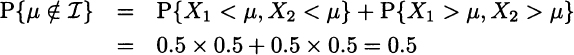
So, the confidence level for I is the complement of this probability, i.e., 50%. Now suppose that we observe X1 = 0 and X2 =0.6. What is the probability that μ is included in the confidence interval I resulting from Eq. (14.16), i.e., P{0 ≤ μ ≤ 0.6}? In general, this question does not make any sense, since μ is a number. But in this specific case, we have some additional knowledge leading to the conclusion that the expected value is included in the interval [0, 0.6] with probability 1. In fact, if X(1) = 0, we may conclude μ ≤ 0.5; by the same token, if X(2) = 0.6, we may conclude μ ≥ 0.1. Since the confidence interval I includes the interval [0.1, 0.5], we would have good reasons to claim that P{0 ≤ μ ≤ 0.6} = 1. But again, this makes no sense in the orthodox framework. By a similar token, if we get X1 = 0 and X2 = 0.001, we would be tempted to say that such a small interval is quite unlikely to include μ, but there is no way in which we can express this properly, within the framework of orthodox statistics.
On one hand, the example illustrates the need to make our background knowledge explicit. In the Bayesian framework, it can be argued that unconditional probabilities do not exist, in the sense that probabilities are always conditional on background knowledge and assumptions. On the other hand, we see the need of a way to express subjective views, which may be revised after collecting empirical data. Bayesian estimation has been proposed to cope with such issues.
Leave a Reply