Consider a bar of varying cross-section of uniform strength subjected by a longitudinal stress σ as shown in Figure 12.10. Now consider a small element of axial length δx at a distance of x from smaller end. Let area of cross-section at section x be A and at section x + δx be A + δA. For the element of length δx to be in equilibrium, the total downward force must be equal to the total upward force acting on it.
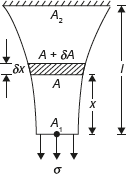
Figure 12.10 Varying Cross-section Bar of Uniform Strength
Weight of length δx + Tensile stress at section x × Area at section x = Tensile stress at section (x + δx) × Area at section (x + δx)
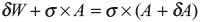
Here, δW is vertical weight due to weight of free body = ρ × g × A × δx where ρ is the density of material of the bar.
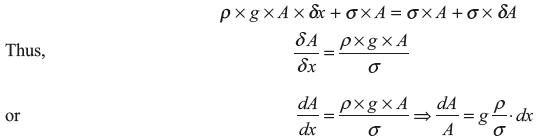
On integration, between area A1 and A
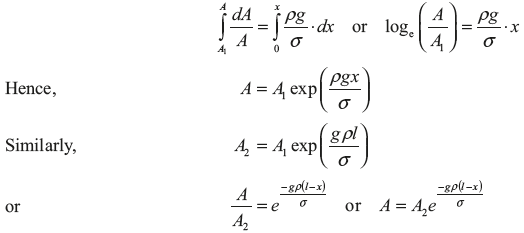
Let de be the extension in a small length dx.
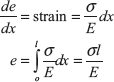
Example 12.6: A bar of uniform strength is shown in Figure 12.11.
Its length is 5 m, diameter at bottom edge is 100 mm, weight density of bar is 0.07644 × 10−3 N/mm2. It is subjected to a uniform stress 0.6 N/mm2. Find the diameters at the top and at the half of its length.
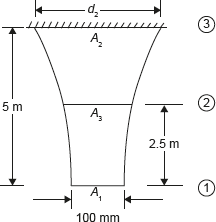
Figure 12.11 Bar of Uniform Strength
Solution:
Given: d = 100 mm, l1 = 5 m, σ = 0.6 N/mm2, pg = 0.07644 × 10−3 N/mm2.
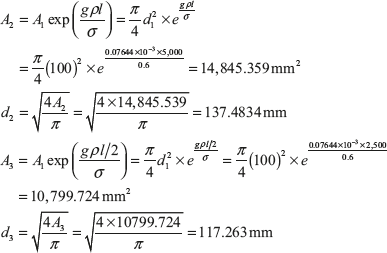
Leave a Reply