The dot diagram is a useful data display for small samples, up to (say) about 20 observations. However, when the number of observations is moderately large, other graphical displays may be more useful. A stem‐and‐leaf display or stem‐and‐leaf plot, also called a stemplot, is a device for presenting quantitative data in a graphical format, similar to a histogram, to assist in visualizing the shape of a distribution. They evolved from Arthur Bowley’s work in the early 1900s and are useful tools in exploratory data analysis. Stemplots became more commonly used in the 1980s after the publication of John Tukey’s book on exploratory data analysis in 1977 (Tukey 1977).
A stem‐and‐leaf display often refers to another chart type. A simple stemplot may refer to plotting a matrix of y values onto a common x‐axis, and identifying the common x value with a vertical line, and the individual y values with symbols on the line (Wild and Seber 2000).
Unlike histograms, stem‐and‐leaf displays retain the original data to at least two significant digits, and put the data in order, thereby easing the move to order‐based inference and nonparametric statistics.
A basic stem‐and‐leaf display contains two columns separated by a vertical line. The left column contains the stems and the right column contains the leaves.
Constructing a Stem‐and‐Leaf Display
EXAMPLE 8.3
To construct a stem‐and‐leaf display, the observations must first be sorted in ascending order: this can be done most easily if working by hand by constructing a draft of the stem‐and‐leaf display with the leaves unsorted, then sorting the leaves to produce the final stem‐and‐leaf display. Here is the sorted set of data values that will be used in the following example:
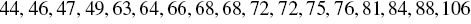
Next, it must be determined what the stems will represent and what the leaves will represent. Typically, the leaf contains the last digit of the number and the stem contains all of the other digits. In the case of very large numbers, the data values may be rounded to a particular place value (such as the hundreds place) that will be used for the leaves. The remaining digits to the left of the rounded place value are used as the stem. In this example, the leaf represents the ones place and the stem will represent the rest of the number (tens place and higher).
The stem‐and‐leaf display is drawn with two columns separated by a vertical line. The stems are listed to the left of the vertical line. It is important that each stem is listed only once and that no numbers are skipped, even if it means that some stems have no leaves. The leaves are listed in increasing order in a row to the right of each stem.
It is important to note that when there is a repeated number in the data (such as two 72s) then the plot must reflect such (so the plot would look like 7 | 2 2 5 6 7 when it has the numbers 72 72 75 76 77).
| Stem | Leaf | Frequency |
| 4 | 4 6 7 9 | 4 |
| 5 | 0 | |
| 6 | 3 4 6 8 8 | 5 |
| 7 | 2 2 5 6 | 4 |
| 8 | 1 4 8 | 3 |
| 9 | 0 | |
| 10 | 6 | 1 |
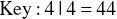
Rounding may be needed to create a stem‐and‐leaf display. Based on the following set of data, the stemplot below would be created:
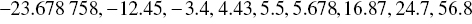
For negative numbers, a negative is placed in front of the stem unit, which is still the value X/10. Non‐integers are rounded. This allowed the stem‐and‐leaf plot to retain its shape, even for more complicated data sets as in this example below:
| Stem | Leaf | Frequency |
| −2 | 3 | 1 |
| −1 | 2 | 1 |
| −0 | 3 | 1 |
| 0 | 4 6 6 | 3 |
| 1 | 7 | 1 |
| 2 | 5 | 1 |
| 3 | 0 | |
| 4 | 0 | |
| 5 | 7 | 1 |
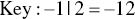
The stem‐and‐leaf diagram displays make it relatively easy to find data features such as percentiles, quartiles, and median. The median is a measure of central tendency that divides the data into two equal parts, half below the median and half above. If the number of observations is even, the median is halfway between the two central values.
Leave a Reply