Size and power of a test

In the elementary theory of hypothesis testing we consider a null hypothesis such as

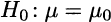
against the alternative H_a : μ ≠ μ₀. Given a sample X = (X₁,…, X_n), we considered a rejection region C related to two tails of a standard normal or t distribution. In this case, it is quite easy to evaluate the probability of a type I error

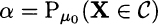
This is just the probability that, even though the null hypothesis is true, the test statistic falls in the rejection region. The notation P_μ0 refers to the fact that we associate a probability distribution with the unique value μ₀ considered in the null hypothesis. But which probability distribution should we consider when the null hypothesis is H₀ : μ ≤ μ₀?

To generalize the analysis, let us consider a vector of parameters θ and a null hypothesis of the form

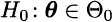
versus the alternative

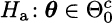
Here Θ₀ is an arbitrary region, and  is its complement. The vector of parameters could be subject to additional restrictions; for instance, a subset of parameters could take only nonnegative values. Let us denote the set of feasible values of parameters by Θ; clearly, . In the first case above the set Θ₀ is a singleton, Θ₀ = {μ₀}, and we speak of a simple hypothesis; otherwise, we have a composite hypothesis.

DEFINITION 9.17 (Size of a test) We say that a test with rejection region C has size α if

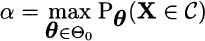
Of course, the size of a test is essentially another name for the significance level. From its definition, we see that α is related to the worst-case distribution in terms of type I errors. Since we want to be conservative, it is natural to give priority to type I errors by keeping α reasonably small. However, given a test size, we should find a test minimizing the probability of a type II error. If , the probability of type II error is

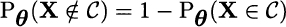
Note that

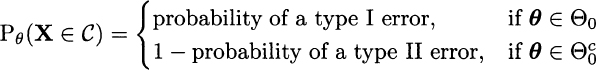
DEFINITION 9.18 (Power of a test) The power function for a test with rejection region C is a function of θ, defined as

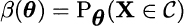
Note that the power of a test is a function, as it depends on the true value the unknown parameter vector; hence, in a practical setting, we are not able to find a single value giving the power of the test. Still, we may observe that the ideal power function is 0 for θ ∈ Θ₀ and 1 for . This ideal power function cannot be obtained in practice, but we can look for tests that have maximal power when . The theory of optimal, or most powerful, tests is developed in the context of mathematical statistics and it relies on systematic ways to devise testing procedures. We outline one of them in the next section.