From a qualitative perspective, the form of the confidence interval (9.10) suggests the following observations:
- When the sample is very large, we may use the quantiles z1−α/2 from the standard normal distribution, since the t distribution tends to a standard normal, when the degrees of freedom go to infinity.
- The larger the confidence level 1 − α, the larger the confidence interval; in other words, a wider interval is required to be “almost sure” that it includes the true value (in the sense that we have just clarified!).
- The confidence interval is large when the underlying variability σ of the observations is large.
- The confidence interval shrinks when we increase the size of the sample. Actually, it might be the case that the interval gets larger by adding a few observations, if these additional data result in a larger sample standard deviation S, but this is a pathological behavior that we may observe if we add a few observations to a small sample.
The last statement is quite relevant, and is related to an important issue. So far, we have considered a given sample and we have built a confidence interval. However, sometimes we have to go the other way around: Given a required precision, how large a sample should we take? One way of formalizing the issue is the following. Say that we require the following condition on the maximum absolute error:
Clearly, we can obtain only a probabilistic guarantee: Condition (9.11) should hold with confidence level 1 − α. This requirement can be rewritten as a pair of inequalities, since 
could be positive or negative:
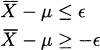
The two inequalities may be rearranged as
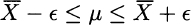
from which we see that 
is just the half-length of the confidence interval. Hence, we should find a sample size n as follows:
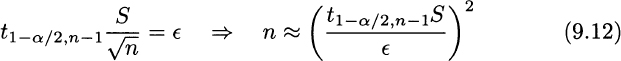
The careful reader will certainly be dissatisfied with the last equation: How can we find the sample size n before sampling, if this requires knowledge of sample standard deviation S, which is obviously known only after sampling? Furthermore, n depends on n itself, since (9.12) defines n as a function the quantile t1−α/2, n−1 that we should use. The standard way out of this dilemma is as follows:
- Assume that n should be large enough to warrant use of quantiles z1−α/2 of the standard normal, which suppresses the circular dependence on n.
- Take an exploratory sample to find a rough estimate S, which can be used to find the total sample size n. Clearly, there is no guarantee that, after completion of the overall sampling, the initial estimate S will turn out to be close to the new estimate based on the whole sample. So, we should take the exploratory sample, add the tentative number of observations, and then check again, possibly repeating the procedure.
Example 9.9 A sample of size n = 25, taken from a normal population, yields
The resulting 95% confidence interval is (101.8212, 141.8368) which is too large for your purposes, and you would like to take a sample large enough to guarantee, with confidence level 95%, that the absolute error is smaller than 1. The required sample size would be
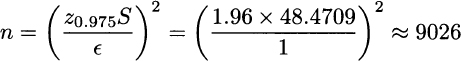
The example illustrates the potentially high price of precision when variability is large. To get a better feeling for this issue, let us say that when sample size is n, the half-width of the confidence interval is H; how large should a sample size n′ be, in order to ensure H′ = H/10, while keeping the same confidence level? Note that this requirement corresponds to an improvement of one order of magnitude in precision. Using the formula for the half-width we see that
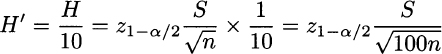
which implies n′ = 100n. Hence, to improve precision by one order of magnitude, the sample size must increase by two orders of magnitude. The reason is that the effect of increasing sample size is “killed” by the square-root function 
, which is concave.
We emphasize again that in this section we have just derived a confidence interval for the expected value of a normal distribution. Asymptotic results and the central limit theorem allow us to apply Eq. (9.10) as an approximation for large samples, but it is sometimes necessary or advisable to take a different route when estimating other parameters, such as variance, or when dealing with different distributions. In Section 9.4 we illustrate some generalizations, while keeping the treatment at an elementary level. In Section 9.9 we consider parameter estimation within a more systematic and general framework.
Leave a Reply