Say that we are in charge of managing the inventory of a component, whose supply lead time is 2 weeks. Weekly demand is modeled by a normal random variable with expected value 100 and standard deviation 20 (let us pretend that this makes sense). If we apply a reorder point policy based on the EOQ model, we should order a fixed quantity whenever the inventory level falls below a reorder point R.24 How can we set R in order to achieve a 95% service level?
The service level in this case is the probability of not having a stockout during the delivery lead time. Note that we may run out of stock during the time window between the instant at which we issue the order to our supplier and the time instant at which items are received and inventory is replenished. Hence, we should consider the probability that demand during lead time does not exceed the reorder point R, which should be set in such a way that
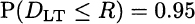
If we assume that weekly demand is normal, then we should just compute a quantile from the normal distribution again. If demands in two consecutive weeks are independent, then the distribution of the demand during lead time is normal with parameters
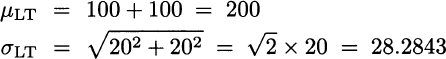
Since z0.95 = 1.6449, we should set
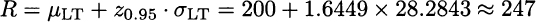
Note that, if there were no risk, we would just set R = 200. The additional 47 items we keep on stock are a safety stock. To reduce safety stock, and save money related to holding inventory, we should reduce demand uncertainty and/or lead time. This is precisely one of the cornerstones of the so-called Toyota approach, which was originally applied within the automotive industry to car manufacturing; its extension to other industries resulted in the well-known just-in-time philosophy.
Leave a Reply