The sample mean is a well-known concept from descriptive statistics:
If data come from a legitimate random sample, sample mean is a statistic. A natural use of sample mean is to estimate the expected value of the underlying random variable, that is unknown in practice. It is important to understand what we are doing: We are using a random variable as an estimator of some unknown parameter, which is a number. The realization of that random variable, the estimate, is, of course, a number, but we will typically get different numbers whenever we repeat the sampling procedure. They may even be quite different numbers.
Table 9.1 Sample means from normal distributions.a
a Column headers report expected value μ and standard deviation σ for the underlying distribution, as well as the sample size n; 10 random samples are drawn for each setting of these parameters.
Example 9.4 In Table 9.1 we show the realized value of the sample mean in ten samples from a normal distribution.2 The first column shows a lot of variability in the sample mean. This is hardly a surprise, considering that the standard deviation, σ = 20, is twice as much as the expected value, μ = 10, and the sample size is rather small, n = 10. If sample size is increased considerably (n = 1,000,000), we get the second column, which is affected by much less variability. This also happens if we take a small sample from a distribution with small standard deviation, σ = 0.2, as shown in the third column.
The example shows that if we use a random variable to estimate a parameter, variability of the estimator is an obvious issue. We consider the desirable properties of an estimator in greater depth in Section 9.9, but two obvious features are as follows:
- The estimator should be unbiased, i.e., its expected value should be the value of the unknown parameter that we wish to estimate.
- The variability of the estimator should be as small as possible, for a given sample size.
Clearly, we should be interested in the distribution of any sample statistic we use. In more detail, given the probability distribution of the i.i.d. random variables Xi, i = 1,…, n, in the sample, the least we can do is to determine the expected value and variance of sample statistics which are relevant for our analysis; if possible, we should also find their exact distribution.
Example 9.5 (Expected value and variance of the sample mean) Consider a sample consisting of i.i.d. variables Xi with expected value μ and variance σ2. In Section 7.7 we used properties of sums of independent random variables to prove that
We repeat the derivation of these formulas to emphasize the role of the i.i.d. assumption. Independence plays no role in deriving Eq. (9.2), but we do assume that variables are identically distributed. This equation shows that sample mean is indeed an unbiased estimator of the unknown parameter μ. Equation (9.3) shows that the larger the sample size, the lower the variance of the sample mean, as both Table 9.1 and intuition suggest. However, intuition is not enough because it does not clarify the essential role of independence in this. In the limit, if all of the Xi were perfectly correlated, they would be the same number, and increasing the sample size would be of little use.
This example is also useful for understanding the basic framework of orthodox statistics. The expected value μ is an unknown number, and we will use random samples to draw inferences about it. On the contrary, in the Bayesian framework,3 probability distributions are associated with the parameters; these distributions may be used to model a priori knowledge or subjective opinions that we might have. Subjective opinions play no role in the orthodox framework.
The example shows that it is fairly easy to come up with essential properties of the sample mean, but what about its distribution? Unfortunately, there is little we can say in general, as we know that summing identically distributed variables does not yield an easy distribution in general. From Section 7.7 we know that if we sum uniform or exponential variables, we do not get uniform or exponential variables, respectively, even if we assume independence. However, we recall two essential results:
- If we sample from a normal distribution, i.e., if variables Xi are normal, then the sample mean will be exactly normal, since the sum of jointly normal variables is itself normal.
- If we sample from a generic distribution and the sample size is large enough, the central limit theorem4 tells us that the sample mean will tend to a normal random variable. In particular, the distribution of the standardized statistic
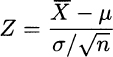tends to a standard normal.
The central limit theorem is fairly general and plays a key role in inferential statistics, but in some cases it is better to exploit the structure of the problem at hand.
Example 9.6 (Sampling from a Bernoulli population) Consider a qualitative variable referring to a property that may or may not hold for an individual of a population. If we sample from that population, we are typically interested in the fraction p of the population, for which the property holds. Let Xi be a random variable set to 1 if the observed individual i enjoys the property, 0 otherwise. We immediately see that we are sampling a Bernoulli population; i.e., the random variables Xi are Bernoulli distributed, with a parameter p ≡ P(X = 1) that we wish to estimate.
Since we are summing n independent Bernoulli variables Xi with expected value p, what we get is related to a binomial random variable Y. From Section 6.5.5, we know that
Equation (9.4) tells us that we may estimate the fraction p by just counting the fraction of the sample that enjoys the following property:
Equation (9.5) tells us how the estimate of the expected value also yields an estimate of variance, 
The case of a Bernoulli population is somewhat peculiar, since there is only one parameter that yields both expected value and variance. In general, if variance is a distinct parameter σ2, we are in trouble when trying to exploit Eq. (9.3), since it relies on another unknown parameter σ that we have to estimate.
Leave a Reply