The properties of formation waters are affected by temperature, pressure, and the quantity of solution gas and dissolved solids, but to a much smaller degree than crude oils. The compressibility of the formation, or connate, water contributes materially in some cases to the production of volumetric reservoirs above the bubble point and accounts for much of the water influx in water-drive reservoirs. When the accuracy of other data warrants it, the properties of the connate water should be entered into the material-balance calculations on reservoirs. The following sections contain a number of correlations adequate for use in engineering applications.
Formation Volume Factor
McCain28 developed the following correlation for the water formation volume factor, Bw (bbl/STB):

where
ΔVwt= – 1.00010 × 10–2 + 1.33391 × 10–4 T + 5.50654 × 10–7 T2
ΔVwp= – 1.95301 × 10–9 pT – 1.72834 × 10–13 p2T – 3.58922 × 10–7 p – 2.25341 × 10–10 p2
T = temperature, °F
p = pressure, psia
For the data used in the development of the correlation, the correlation was found to be accurate to within 2%. The correlation does not account for the salinity of normal reservoir brines explicitly, but McCain observed that variations in salinity caused offsetting errors in the terms ΔVwt and ΔVwp. The offsetting errors cause the correlation to be within engineering accuracy for the estimation of the Bw of reservoir brines.
2.5.2 Solution Gas-Water Ratio
McCain has also developed a correlation for the solution gas-water ratio, Rsw (SCF/STB).28 The correlation is

where
S = salinity, % by weight solids
T = temperature, °F
Rswp = solution gas to pure water ratio, SCF/STB
Rswp is given by another correlation developed by McCain as

where
A = 8.15839 – 6.12265 × 10–2 T + 1.91663 × 10–4 T2 – 2.1654 × 10–7 T3
B = 1.01021 × 10–2 – 7.44241 × 10–5 T + 3.05553 × 10–7 T2 – 2.94883 × 10–10 T3
C = –10–7 (9.02505 – 0.130237 T + 8.53425 × 10–4 T2 – 2.34122 × 10–6 T3 + 2.37049 × 10–9 T4)
T = temperature, °F
The correlation of Eq. (2.40) was developed for the following range of data and found to be within 5% of the published data:
1000 < p (psia) < 10,000
100 < T (°F) < 340
Equation (2.41) was developed for the following range of data and found to be accurate to within 3% of published data:
0 < S (%) < 30
70 < T (°F) < 250
2.5.3 Isothermal Compressibility
Osif developed a correlation for the water isothermal compressibility, cw, for pressures greater than the bubble-point pressure.29 The equation is
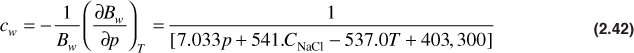
where
CNaCl = salinity, g NaCl/liter
T = temperature, °F
The correlation was developed for the following range of data:
1000 < p (psig) < 20,000
0 < CNaCl (g NaCl/liter) < 200
200 < T (°F) < 270
The water isothermal compressibility is strongly affected by the presence of free gas. Therefore, McCain proposed using the following expression for estimating cw for pressures below or equal to the bubble-point pressure:28
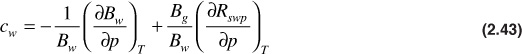
The first term on the right-hand side of Eq. (2.43) is simply the expression for cw in Eq. (2.42). The second term on the right-hand side is found by differentiating Eq. (2.41) with respect to pressure, or
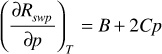
where B and C are defined in Eq. (2.41).
In proposing Eq. (2.43), McCain suggested that Bg should be estimated using a gas with a gas gravity of 0.63, which represents a gas composed mostly of methane and a small amount of ethane. McCain could not verify this expression by comparing calculated values of cw with published data, so there is no guarantee of accuracy. This suggests that Eq. (2.43) should be used only for gross estimations of cw.
Viscosity
The viscosity of water increases with decreasing temperature and in general with increasing pressure and salinity. Pressure below about 70°F causes a reduction in viscosity, and some salts (e.g., KCl) reduce the viscosity at some concentrations and within some temperature ranges. The effect of dissolved gases is believed to cause a minor reduction in viscosity. McCain developed the following correlation for water viscosity at atmospheric pressure and reservoir temperature28:

where
A = 109.574 – 8.40564 S + 0.313314 S2 + 8.72213 × 10–3 S3
B = 1.12166 + 2.63951 × 10–2 S – 6.79461 × 10–4 S2 – 5.47119 × 10–5 S3 + 1.55586 × 10–6 S4
T = temperature, °F
S = salinity, % by weight solids
Equation (2.44) was found to be accurate to within 5% over the following range of data:
100 < T (°F) < 400
0 < S (%) < 26
The water viscosity can be adjusted to reservoir pressure by the following correlation, again developed by McCain:28
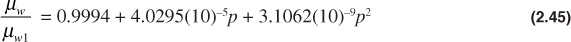
This correlation was found to be accurate to within 4% for pressures below 10,000 psia and within 7% for pressures between 10,000 psia and 15,000 psia. The temperature range for which the correlation was developed was between 86°F and 167°F.
Leave a Reply