Everything up to this point applies to a perfect or ideal gas. Actually there are no perfect gases; however, many gases near atmospheric temperature and pressure approach ideal behavior. All molecules of real gases have two tendencies: (1) to fly apart from each other because of their constant kinetic motion and (2) to come together because of electrical attractive forces between the molecules. Because the molecules are quite far apart, the intermolecular forces are negligible and the gas behaves close to ideal. Also, at high temperatures, the kinetic motion, being greater, makes the attractive forces comparatively negligible and, again, the gas approaches ideal behavior.
When the volume of a gas will be less than what the ideal gas volume would be, the gas is said to be supercompressible. The number, which measures the gas’s deviation from perfect behavior, is sometimes called the supercompressibility factor, usually shortened to the gas compressibility factor. More commonly it is called the gas deviation factor (z). This dimensionless quantity usually varies between 0.70 and 1.20, with a value of 1.00 representing ideal behavior.
At very high pressures, above about 5000 psia, natural gases pass from a supercompressible condition to one in which compression is more difficult than in the ideal gas. The explanation is that, in addition to the forces mentioned earlier, when the gas is highly compressed, the volume occupied by the molecules themselves becomes an appreciable portion of the total volume. Since it is really the space between the molecules that is compressed and there is less compressible space, the gas appears to be more difficult to compress. In addition, as the molecules get closer together (i.e., at high pressure), repulsive forces begin to develop between the molecules. This is indicated by a gas deviation factor greater than unity. The gas deviation factor is by definition the ratio of the volume actually occupied by a gas at a given pressure and temperature to the volume it would occupy if it behaved ideally, or
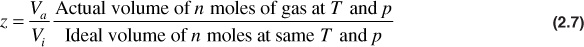
These theories qualitatively explain the behavior of nonideal or real gases. Equation (2.7) may be substituted in the ideal gas law, Eq. (2.4), to give an equation for use with nonideal gases,
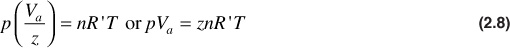
where Va is the actual gas volume. The gas deviation factor must be determined for every gas and every combination of gases and at the desired temperature and pressure—for it is different for each gas or mixture of gases and for each temperature and pressure of that gas or mixture of gases. The omission of the gas deviation factor in gas reservoir calculations may introduce errors as large as 30%.7 Figure 2.1 shows the gas deviation factors of two gases, one of 0.90 specific gravity and the other of 0.665 specific gravity. These curves show that the gas deviation factors drop from unity at low pressures to a minimum value near 2500 psia. They rise again to unity near 5000 psia and to values greater than unity at still higher pressures. In the range of 0 to 5000 psia, the deviation factors at the same temperature will be lower for the heavier gas, and for the same gas, they will be lower at the lower temperature.
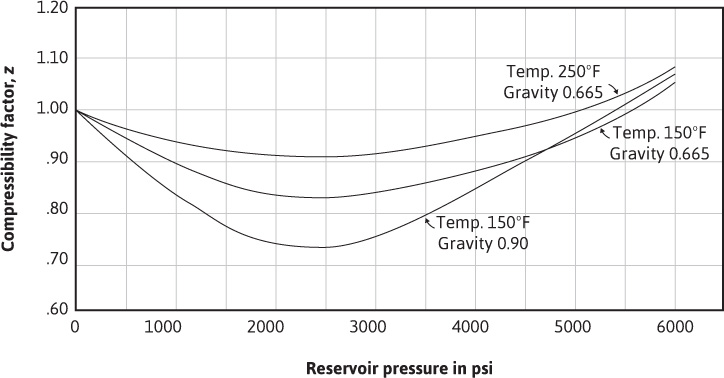
Figure 2.1 Effect of pressure, temperature, and composition on the gas deviation factor.
When possible reservoir fluid samples should be acquired at the formation level, such samples are termed bottom-hole fluid samples, and great care must be taken to avoid sampling the reservoir fluid below bubble-point or dew-point pressure. Without a bottom-hole fluid sample, produced wet gas or gas condensate may be recombined at the surface. This may be accomplished by recombining samples of separator gas, stock-tank gas, and stock-tank liquid in the proportions in which they are produced. The deviation factor is measured at reservoir temperature for pressures ranging from reservoir to atmospheric. For wet gas or gas condensate, the deviation factor may be measured for differentially liberated gas below the dew-point pressure. For reservoir oil, the deviation factor of solution gas is measured on gas samples evolved from solution in the oil during a differential liberation process.
The gas deviation factor is commonly determined by measuring the volume of a sample at desired pressures and temperatures and then measuring the volume of the same mass of gas at atmospheric pressure and at a temperature sufficiently high so that all the material remains in the vapor phase. For example, a sample of the Bell Field gas has a measured volume of 364.6 cm3 at 213°F and 3250 psia. At 14.80 psia and 82°F, it has a volume of 70,860 cm3. Then, by Eq. (2.8), assuming a gas deviation factor of unity at the lower pressure, the deviation factor at 3250 psia and 213°F is
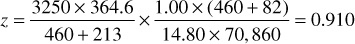
If the gas deviation factor is not measured, it may be estimated from its specific gravity. Example 2.2 shows the method for estimating the gas deviation factor from its specific gravity. The method uses a correlation to estimate pseudocritical temperature and pressure values for a gas with a given specific gravity. The correlation was developed by Sutton on the basis of over 5000 different gas samples.8 Sutton developed a correlation for two distinct types of gases—one being an associated gas and the other being a condensate gas. An associated gas is defined as a gas that has been liberated from oil and typically contains large concentrations of ethane through pentane. A condensate gas typically contains a vaporized hydrocarbon liquid, resulting in a high concentration of the heptanes-plus fractions in the gas phase.
For the associated gases, Sutton conducted a regression analysis on the raw data and obtained the following equations over the range of specific gas gravities with which he worked—0.554 < γg < 1.862:


Sutton found the following equations for the condensate gases covering the range of gas gravities of 0.554 < γg < 2.819:


Both sets of these correlations were derived for gases containing less than 10% of H2S, CO2, and N2. If concentrations of these gases are larger than 10%, the reader is referred to the original work of Sutton for corrections.
Having obtained the pseudocritical values, the pseudoreduced pressure and temperature are calculated. The gas deviation factor is then found by using the correlation chart of Fig. 2.2.
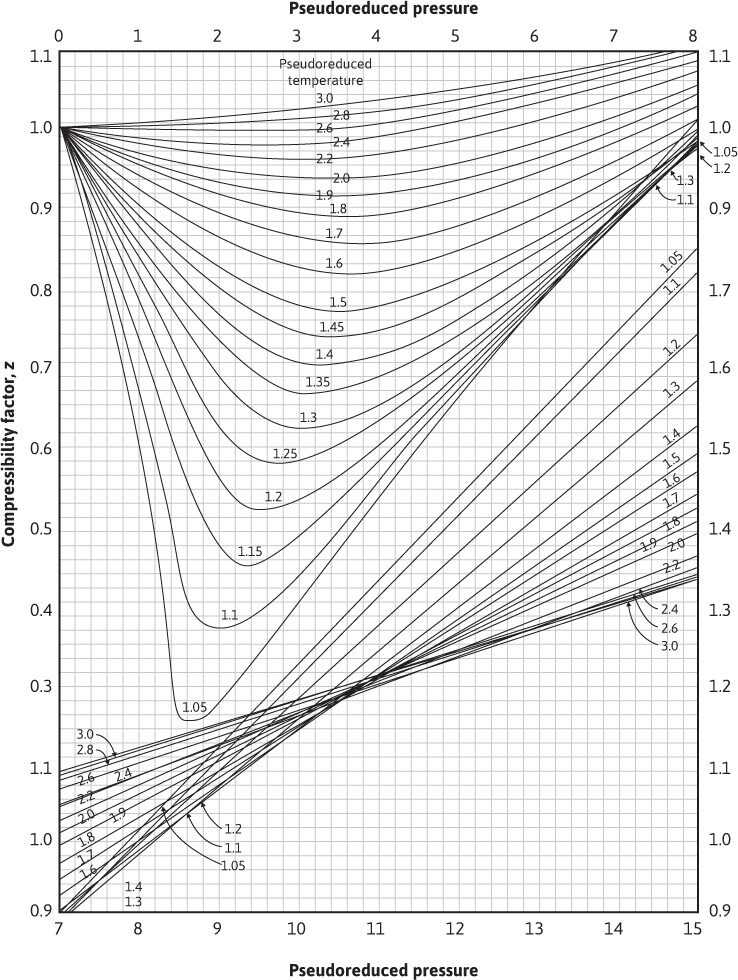
Figure 2.2 Compressibility factors for natural gases (after Standing and Katz, trans. AlME).9
Example 2.2 Calculating the Gas Deviation Factor of a Gas Condensate from Its Specific Gravity
Given
Gas specific gravity = 0.665
Reservoir temperature = 213°F
Reservoir pressure = 3250 psia
Solution
Using Eqs. (2.11) and (2.12), the pseudocritical values are
ppc = 744 – 125.4(0.665) + 5.9(0.665)2 = 663 psia
Tpc = 164.3 + 357.7(0.665) – 67.7(0.665)2 = 372°R
For 3250 psia and 213°F, the pseudoreduced pressure and temperature are
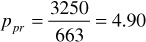
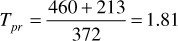
Using the calculated values in Fig. 2.2, z = 0.918.
In many reservoir-engineering calculations, it is necessary to use the assistance of a computer, and the chart of Standing and Katz then becomes difficult to use. Dranchuk and Abou-Kassem fit an equation of state to the data of Standing and Katz in order to estimate the gas deviation factor in computer routines.10 Dranchuk and Abou-Kassem used 1500 data points and found an average absolute error of 0.486% over ranges of pseudoreduced pressure and temperature of
0.2 < ppr < 30
1.0 < Tpr < 3.0
and for
ppr < 1.0 with 0.7 < Tpr < 1.0
The Dranchuk and Abou-Kassem equation of state gives poor results for Tpr = 1.0 and ppr > 1.0. The form of the Dranchuk and Abou-Kassem equation of state is as follows:
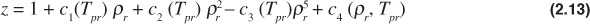
where

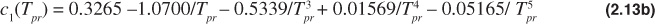
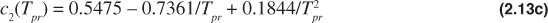
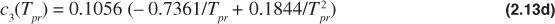
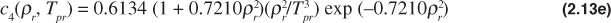
Because the z-factor is on both sides of the equation, an iterative method is necessary to solve the Dranchuk and Abou-Kassem equation of state. Any one of a number of techniques can be used to assist in the iterative method.11 The Excel solver function is a common computer tool to solve these types of iterative problems, and instructions on its use are available in the Help section of the Excel program.
A more accurate estimation of the deviation factor can be made when the analysis of the gas is available. This calculation assumes that each component contributes to the pseudocritical pressure and temperature in proportion to its volume percentage in the analysis and to the critical pressure and temperature, respectively, of that component. Table 2.1 gives the critical pressures and temperatures of the hydrocarbon compounds and others commonly found in natural gases.12 It also gives some additional physical properties of these compounds. Example 2.3 shows the method of calculating the gas deviation factor from the composition of the gas.
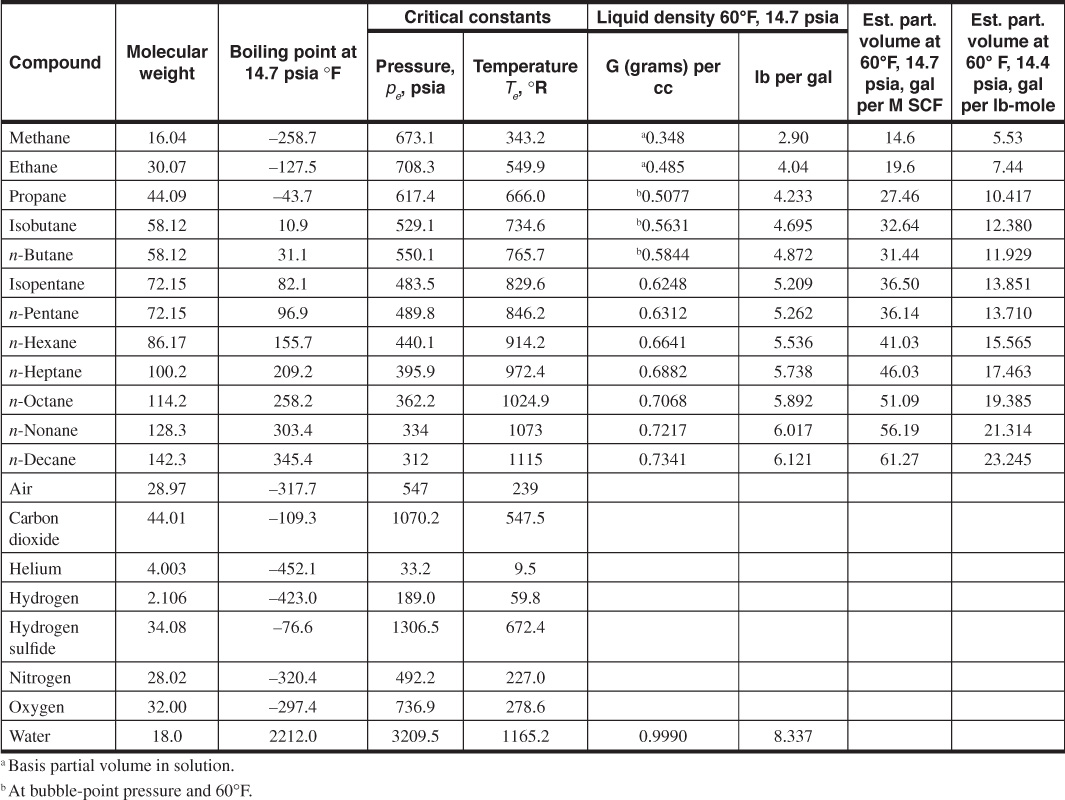
Table 2.1 Physical Properties of the Paraffin Hydrocarbons and Other Compounds (after Eilerts12)
Example 2.3 Calculating the Gas Deviation Factor of the Bell Field Gas from Its Composition
Given
The composition column 2 and the physical data columns 3 to 5 are taken from Table 2.1.
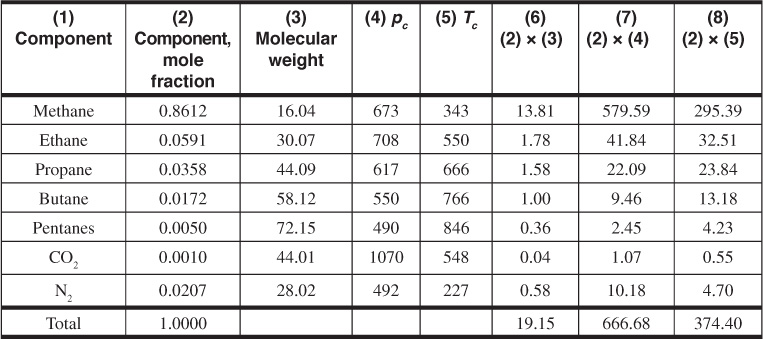
Solution
The specific gravity may be obtained from the sum of column 6, which is the average molecular weight of the gas,
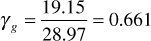
The sums of columns 7 and 8 are the pseudocritical pressure and temperature, respectively. Then, at 3250 psia and 213°F, the pseudoreduced pressure and temperature are
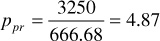
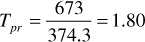
The gas deviation factor using Fig. 2.2 is z = 0.91.
Wichert and Aziz have developed a correlation to account for inaccuracies in the Standing and Katz chart when the gas contains significant fractions of carbon dioxide (CO2) and hydrogen sulfide (H2S).13 The Wichert and Aziz correlation modifies the values of the pseudocritical constants of the natural gas. Once the modified constants are obtained, they are used to calculate pseudoreduced properties, as described in Example 2.2, and the z-factor is determined from Fig. 2.2 or Eq. (2.13). The Wichert and Aziz correlation equation is as follows:
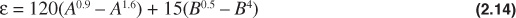
where
A = sum of the mole fractions of CO2 and H2S in the gas mixture
B = mole fraction of H2S in the gas mixture
The modified pseudocritical properties are given by


Wichert and Aziz found their correlation to have an average absolute error of 0.97% over the following ranges of data: 154 < p (psia) < 7026 and 40 < T (°F) < 300. The correlation is good for concentrations of CO2 < 54.4% (mol %) and H2S < 73.8% (mol %).
Leave a Reply