Let T1 is tension in tight side of the belt
T2 is tension in slack side of the belt
θ is angle of lap of belt over the pulley
μ is coefficient of friction between the belt and pulley
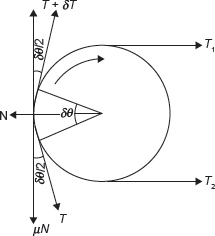
Figure 15.5 Tensions in Belt
Consider a short length of belt subtending an angle δθ at the centre of the pulley as shown in Figure 15.5.
Let N is a normal reaction between the element length of a belt and pulley
δT is increase in tension in tight side than that on slack side
T + δT is tension on the tight side of the element
Resolving the force in tangential direction,
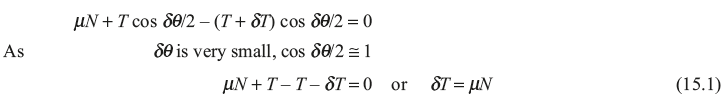
Resolving the force in radial direction,
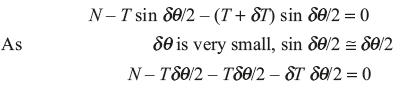
Neglecting the product of two small quantities
From Eqs (15.1) and (15.2), 
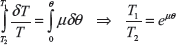
In V-belt, 
, where α is the angle made by V-section of the belt.
Leave a Reply