QUANTUM TUNNELING

chSo far, our analysis of the particle-in-a-box problem has assumed that the barriers around the box are infinite:

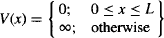
which allowed us to force the particle to always be within the box. We were thus able to make Ψ = 0 for x ≤ 0 and x ≥ L.

What would happen if the walls didn’t have infinite potential? Well, the interesting thing about waves, which include solutions to Schrödinger’s equation for the probability of finding particles at a certain position, is that they are spread-out entities that don’t end abruptly when faced with a finite wall or barrier, but instead taper off beyond the obstacle. In the classical mechanics picture of Figure 114a, objects cannot cross regions where their kinetic energy would have to be negative. A ball directed toward a wall will bounce back with no possibility of penetrating the wall. However, as shown in Figure 114b, if the barrier is thin enough, the probability function may extend into the next region. Quantum physics thus predicts there is a chance that a particle trapped behind a barrier without the energy to overcome the barrier may at times appear on the other side of the barrier without overcoming it or breaking it down. This unusual phenomenon is known as “quantum tunneling.”

Figure 114 Quantum tunneling through a barrier. (a) In classical physics, a particle with a certain kinetic energy bounces off a barrier that has a higher energy threshold to be overcome. (b) In quantum physics, however, the wavefunction of a particle extends through a barrier, and there is a certain probability of the particle tunneling to the other side of the barrier. (c) For electromagnetic waves (e.g., light), this means that the barrier reflects much of the energy, but allows some of it to tunnel through.

This is completely counterintuitive for macroscopic systems. Imagine that you are trapped in a jail cell (accused of poisoning cats). You don’t have enough energy to penetrate its walls. Yet, according to quantum physics, there is a certain probability that if you jump against the wall you will disappear from the inside and reappear on the outside leaving the cell’s wall unbroken. Quantum tunneling in this macroscopic example is theoretically possible but unimaginably unlikely, yet it occurs all the time for very small particles all around us. For example, alpha particles—which as you may remember comprise two protons and two neutrons bound together into a particle identical to a helium nucleus—are emitted by an uranium atom when it decays into a thorium atom (²³⁸U → ²³⁴Th + α). In classical physics, the alpha particle is forbidden from escaping, because its energy is too weak to overcome the forces trapping it within the nucleus, but according to quantum mechanics, it has a small (but non-zero) probability of “tunneling” through the barrier and appearing on the other side to escape the nucleus. In fact, quantum tunneling is the process behind all radioactive alpha decay. Alpha particles from the ²⁴¹Am in your smoke detector are constantly being radiated after quantum tunneling out of the nucleus. The tunneling process also happens constantly in the sun: hydrogen nuclei in the sun’s core don’t have sufficient energy to overcome the “barrier” of electrical repulsion, yet they fuse together to form helium while releasing vast amounts of energy that keep us alive on earth.

As shown in Figure 114c, the same thing happens to an electromagnetic wave hitting a barrier with finite potential, since we may view it as a large group of photons reaching the obstacle. Some of these photons will tunnel through the barrier and reappear behind it.

A simple experiment to demonstrate the bizarre quantum effect of tunneling can be performed with the Gunnplexer microwave units we built in (Figure 12). For this experiment, we must remember that classical optics tells us that electromagnetic waves approaching a dielectric–air boundary at an angle greater than the critical angle for total internal reflection are totally reflected inside the material. For example, if you shine a laser from inside a pool toward the outside of the pool, the laser beam will be completely reflected back into the pool if the laser is aimed beyond a critical angle. Beyond this critical angle there is no refracted wave. This is equivalent to the classical mechanics prohibition of objects crossing regions where their kinetic energy does not suffice to penetrate the barrier (Figure 114a).

When the λ = 2.85-cm microwaves from a Gunnplexer are directed into a prism made of paraffin or other dielectric material, they will be completely reflected for angles of incidence greater than the critical angle, as shown in Figure 115a. From the classical physics point of view, it is obvious that microwave receiver 2 should not detect any microwave photons from its location behind the reflective barrier. However, a solution to Maxwell’s wave equation does exist at the point of microwave receiver 2. The solution indicates that the electric field of the electromagnetic wave will decay exponentially at the interface, rather than oscillate in a sine-wave fashion as it does inside the prism. The meaning of the finite electric field beyond the interface is ignored by classical physics, because it is abstract and seemingly absurd, since Maxwell’s equations would show that the electric field doesn’t oscillate beyond the reflective barrier.³⁶

Figure 115 Internal reflection of microwaves (photons with λ ≈ 3 cm) in a prism. (a) Normal internal reflection in which photons incident on the paraffin–air interface are completely reflected toward microwave detector 1, allowing no photons to be transmitted for detection by microwave receiver 2. (b) Some of the photons tunnel through the forbidden region when a second prism is placed at less than one wavelength away from the reflecting surface.

What is interesting is that placing a second prism in the forbidden region, within one wavelength of the reflective barrier, frustrates the total internal reflection, allowing some of the microwaves to be transmitted through the barrier. From the perspective of quantum physics, the wave equation past the barrier is valid and describes the probability of finding photons that tunneled across the barrier. Thus, solving Maxwell’s equation inside the second prism produces an oscillating electric field that can be detected by the second microwave detector. This proves that some of the photons must tunnel through the gap between the two prisms (a forbidden region) and reappear when passing through the second prism.

Okay, so let’s see how to use the Gunnplexer modules to experiment with photons that vanish and instantly reappear over an inch away! You should build two prisms, as shown in Figure 116a. We first cut a 30°/60°/90° foam-board triangle (sides measuring 5-in., 8.66-in., and 10-in.) to use as the base. We made the walls out of 1/16-in.-thick balsa wood. We then filled each form with around 700 g of poly-propylene pellets (roughly 1/8-in. diameter Poly-Pellets^® made by Fairfield, Danbury, CT) sold at the craft store as stuffing for plush toys.

Figure 116 This simple arrangement makes it possible to measure the quantum tunneling of microwave photons through a large air gap. (a) We built the frames for our prisms from foam board for the base and top, and thin balsa wood for the walls. The prisms are filled with poly-propylene pellets. The “white” prism has the top removed to show the pellets. (b) As expected from a prism, the signal refracts at angle according to Snell’s Law. (c) and (d) Virtually no signal is detected at angles greater than the critical angle. (e) However, placing a second prism less than one wavelength away from the reflecting surface frustrates the total internal reflection, allowing some microwave photons to tunnel through the forbidden region.

Place one of the prisms on the goniometer stand (the one we built in shown in Figure 17) so the 8.66 in. face rests against the transmitter’s horn antenna, and measure the angle at which the goniometer needs to be rotated to detect the strongest signal. This angle should obey Snell’s Law, which states that the ratio of the sines of the angles of incidence and refraction (θ₁, θ₂) is equal to the inverse ratio of the indices of refraction (n₁; n₂)

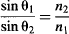
Assuming that the refraction angle for air is 1.00, what is the index of refraction that you measure for the polypropylene pellets? While scanning with the goniometer, you probably noticed that virtually no signal escapes the prism, except at the prism’s specific angle of refraction (Figure 116b).

Place the Gunnplexers and prism on a table, as shown in Figure 116d. You should find that almost no signal can be detected by a receiver placed in line with the transmitter when the prism is in place. In addition, the signal is completely reflected by the prism’s long side, as shown in Figure 116c. It is thus impossible to explain how microwave photons should suddenly make an appearance by just adding a prism to the setup of Figure 116d, when the prisms are not even in contact with each other. However, using quantum mechanics, we find that the wave equation past the barrier is valid and describes the probability of finding photons that tunneled across the barrier. Placing a permitted region (the second prism) across the barrier allows photons to tunnel across the forbidden region between the two permitted regions (the two prisms).