QUANTUM TELEPORTATION

It would seem that it is impossible to communicate or manipulate an unknown quantum state without destroying its fragile nature and causing its collapse. Furthermore, we have already seen that any measurement, however mild, causes Heisenberg’s Uncertainty Principle to kick in and cause a random change in the system being measured.

In 1993, scientists Charles H. Bennett of IBM; Gilles Brassard, Claude Crépeau, and Richard Jozsa from the University of Montreal; Asher Peres from the Technion in Israel; and William K. Wootters of Williams College proposed that entanglement could be used to get around the limitations imposed by Heisenberg’s Uncertainty Principle in order to communicate an unknown quantum state.⁵⁷ Their proposal was to teleport^‡‡‡ the quantum state of a particle from one place to another through the use of an auxiliary pair of entangled particles and a classical communications channel.

The idea, shown in the diagram of Figure 152, is as follows: the transmitter—commonly referred to as Alice—is given a photon with unknown state x to be tele-ported to a receiver—Bob—without either of them learning anything about x’s state. Expecting this task, Alice and Bob previously shared an entangled pair of photons, which they have kept undisturbed. Alice performs a joint measurement of her entangled photon A and the photon to be teleported (x). However, this joint measurement does not allow Alice to determine the individual polarizations of either A or x, so it is not bound by Heisenberg’s Uncertainty Principle. Instead, it tells Alice only what the relative polarization between A and x is. For example, Alice may find that A and x have the same polarization, or that their polarizations are perpendicular to each other, or that they are at an intermediate angle. This measurement, known as a Bell-state measurement, destroys x, but not the quantum connection between A and B. In fact, Bob’s photon (B) instantaneously acquires a state that incorporates the unknown state of x. The teleportation is completed when Alice tells Bob how to rotate the polarization of his photon to remove the original state of the entangled pair, leaving Bob with an exact replica of the original photon x. Again, neither Alice nor Bob know anything about x’s state, allowing it to remain in quantum superposition.

Figure 152 The unknown state of photon x can be teleported by Alice to Bob if they share an auxiliary entangled-photon pair. Alice first performs a Bell-state measurement between her entangled photon (A) and the photon to be teleported (x). Bob’s photon instantaneously acquires a state that incorporates the unknown state of x. Alice uses a classical communication channel to tell Bob how to rotate the polarization of his photon based on the results of the Bell-state measurement to produce a perfect replica of photon x. However, the state of x remains unknown, thus achieving teleportation.

The last procedure in the teleportation sequence requires Alice to tell Bob the results of her Bell-state measurement via a classical channel (e.g., a letter, e-mail message, or phone call). Only after receiving this information via a normal communications channel (which does not exceed the speed of light), can Bob potentially read and use the polarization state that was conveyed instantaneously via “spooky action at a distance” between the entangled pair of photons, thus preserving Einstein’s limit on the speed at which information can be passed between two observers.

Let’s take a look at the teleportation protocol in more detail. Suppose that photon x is a qubit in superposition of states:

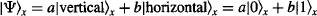
where the bra-ket notation  simply denotes that the system or particle n has the state Ψ.

At the same time, Alice and Bob have a pair of entangled photons A and B. Assuming that we use a type II BBO crystal to generate the entangled pair, the entanglement places both photons into a single quantum system AB, where both photons have unknown polarization, but their individual polarization is perfectly perpendicular to one another:

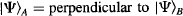
When Alice performs the Bell-state measurement between photons x and A, the entanglement originally shared between Alice’s and Bob’s photons is broken. Instead, Bob’s photon B now takes on a state |Ψ_B that is a superposition of four possible states that combine the original state of x with the original state of A. One of these four random states is already the original state of x, the other three are states in which the polarization of x has been rotated by a certain amount:

1. , the state of Bob’s photon is already identical to the original state of x.

2.  + 90°, the state of Bob’s photon is perpendicular to the original state of x.

3.  + α, the state of Bob’s photon is the original state of x rotated by some angle α.

4.  + β, the state of Bob’s photon is the original state of x rotated by some angle β.

The last two states involve a complex rotation, so let’s not worry about them. They won’t prevent us from understanding the process.

Alice knows which one of the polarization rotations has to be applied by Bob to recreate the original state of x, but Bob doesn’t know it until he receives a conventional message from Alice. Once Bob knows the results of Alice’s Bell-state measurement, he simply uses a polarization rotator (which doesn’t tell him the actual polarization of the photon, it simply adds a certain polarization angle to whatever polarization the photon already had) to perfectly reproduce the state of x.

So, if Alice’s Bell-state measurement in Figure 152 results in case 1, she tells Bob that his photon is already identical to the original state of x. However, if Alice measures case 2, she needs to tell Bob to rotate his photon by 90° to recreate the original state of x. At the end of the procedure, the original photon x at Alice’s end has been destroyed, but its state has been teleported with complete precision to a photon at Bob’s end. Since the photon is completely characterized by its quantum state, teleporting the state is identical to actually teleporting the photon itself.

Bennett et al.’s 1993 teleportation protocol looks simple,⁵⁷ but it took the brilliance of Anton Zeilinger—arguably today’s most prominent experimental quantum physicist—to figure out how to implement it in the real world. It was only in 1997 that Anton Zeilinger’s team, then at the University of Innsbruck in Austria, was able to perform an actual teleportation experiment with the setup shown in Figure 153. This diagram is rather busy, so let’s take our time looking at each part of the system.

Figure 153 In the system developed to perform the first successful teleportation, an entangled pair of photons A and B is produced by a very brief (150 × 10⁻¹⁵ s) laser pulse. One photon from this pair goes to Alice and the second to Bob. The pump pulse is then reflected back into the BBO crystal to produce a second set of entangled photons C and D, but one of them (D) is given a known polarization to create the photon x to be teleported. The second photon (C) is used to indicate the existence of x. Alice conducts a Bell-state measurement between her entangled photon (A) and x (for which she doesn’t know the polarization). Alice tells Bob when both of her detectors fire simultaneously. When this happens, Bob verifies that his entangled photon (B) has the same polarization as x, thus demonstrating successful teleportation.

The process begins with a pulse of UV light produced by a very specialized (and currently very expensive) type of laser.^§§§ The laser’s pulse lasts only 150 fs (150 × 10⁻¹⁵s), which barely suffices to produce one entangled-photon pair (A and B) when sent through a BBO crystal. Instead of dumping the remaining UV light into a beam stop, as we did before, the pulse is reflected back by a mirror into the BBO crystal to produce a second set of entangled photons C and D very shortly after A and B are formed.

A and B are shared between Alice and Bob as the auxiliary entangled photons required for teleportation. Photon D is passed through a polarizer to produce a photon to be teleported (x) for which we—but importantly neither Alice nor Bob—know the polarization. Passing D through a polarizer destroys its entanglement with C, but this is not important, because C is used only to tell the system that x is available for teleportation.

So, passing the brief laser pulse through the nonlinear crystal has given us four almost simultaneous photons: the pair that remains entangled (A and B) are sent to Alice and Bob. The other pair is used to create x and a trigger signal for the teleportation system.

The Bell-state measurement proved to be the most difficult challenge for Zeilinger’s team. The idea is that the two photons to be measured jointly must arrive at exactly the same time to a beam splitter. The photons have three ways of exiting the beam splitter: they can both exit through one port, they can both exit through the other port, or they can each exit through separate ports.

We won’t go into the mathematics of the Bell-state measurement, but suffice it to say that the photons exit through different beam-splitter ports only 25% of the time, and when this happens the Bell state measurement indicates that |Ψ_x = |Ψ_B. That is, the state of Bob’s photon has been converted to be identical to the original state of x. The other 75% of the time, photons exit together through one or the other port of the beam splitter, indicating that some rotation has to be applied to Bob’s photon to turn it into a photon with the same state as x.

The special case in which . is called “lucky” by Zeilinger’s team. It happens whenever a photon is detected in each of Alice’s SPCMs as reported by her coincidence counter, in which case we know that Bob’s photon must have the same state as x without any need for further processing. As such, analyzing B through a PBS (Bob) should demonstrate that B has the same polarization as the one we gave x, proving successful teleportation.

For example, if we set the polarizer to vertical, x is vertical (although neither Alice nor Bob know it), and Bob’s photon should always exit the PBS’s vertical port whenever Alice’s coincidence counter indicates the “lucky” case. On the other hand, if the polarizer is set to horizontal, Bob’s photon should only exit through the PBS’s horizontal port when Alice detects a “lucky” coincidence.

As you can see, this system was able to measure only one of the four possible Bell states, so it could only teleport those photons that totally by chance would produce the “lucky” state. Even under those conditions, the experiment wasn’t perfect because it produced only 80% detections of the correct state on Bob’s detectors. However, this was good enough to prove the concept, given that without teleportation happening, a detection rate of only 50% would have been expected.

One of the major issues for effective teleportation is that Alice’s entangled photon (A) and the photon to be teleported (x) must reach the beam splitter at exactly the same time, because the Bell-state measurement requires that the photons not be identifiable from each other. Even a small difference in time of arrival would—in principle—act as a path labeler, identifying which photon (A or x) ended up at which detector. The incredibly short pump laser pulse is used to produce almost simultaneous photons, and their time of arrival can be equalized by making each photon travel the right distance before arriving at the beam splitter. However, even careful calibration of the paths was not sufficient to ensure simultaneous arrival of the photons, so a very clever trick suggested by Marek Zukowski of the University of Gdansk in Poland was incorporated by Zeilinger’s team.

The idea is to pass photons A and x through very narrow band-pass filters that pin down the frequency of the photons very precisely. As you may remember Heisenberg’s Uncertainty Principle will smear the photons in time, making it easier to ensure that both photons reach the beam splitter simultaneously without any possibility of being identified by their time of arrival.

More recently, in 2004, Anton Zeilinger and his group at the University of Vienna, performed successful photon teleportation between laboratories located on two different sides of the river Danube at a distance of 600 m from each other.^58,49 The basic components of the system are shown in Figure 154. Besides the large separation between Alice and Bob, this experiment incorporated more comprehensive measurement of the Bell state, as well as an electro-optic modulator to rotate Bob’s photon according to the results of Alice’s Bell-state measurement.

Figure 154 This setup was used by Anton Zeilinger’s group at the University of Vienna to teleport photons at a distance of 600 m under the Danube River. Besides the large separation between Alice and Bob, this experiment incorporated an electro-optic modulator to rotate Bob’s photon according to the results of Alice’s Bell-state measurement.

The setup is conceptually similar to the one in Figure 153, but much of the photons’ travel takes place inside optical fibers instead of free air. In fact, the critical beamsplitting for the Bell-state measurement is done in a type of all-fiber beam splitter built by thermally tapering and fusing two optic fibers so that their cores come into intimate contact. In addition, the entangled photon sent to Bob from the entangler travels via a long optical fiber laid along a utilities tunnel under the River Danube.

You may see that Alice now has four SPCMs looking at the outputs of two PBSs instead of just two SPCMs detecting photons coming directly out of the Bell-state measurement beam splitter. This configuration allows Alice to distinguish two of the four possible Bell states. Since light travels more slowly through fiber than the radio message travels through air, Bob has time to use the results of Alice’s measurements to rotate the polarization of his photon. He does it with an electro-optic modulator, which contains a crystal that rotates the polarization as a function of applied voltage. If Alice tells Bob that , his photon is already identical to the original state of x, and he doesn’t apply any voltage to the electro-optic modulator. On the other hand, if the result of the Bell-state measurement indicates that , Bob applies a high voltage to the electro-optic modulator to rotate his photon by 90°. This manages to teleport a maximum of 50% of the photons, instead of the 25% possible using only the “lucky” state.

Besides demonstrating that teleportation works over greater distances than on a lab breadboard, the most significant part of this experiment was that the fiber-optic lines were routed under real-world conditions—just as a telecommunications optical fiber would be. In the case of the Danube experiment, the optical fiber was sent through an underground sewage pipe tunnel, which exposed the fiber-optic link to temperature fluctuations, vibrations, and other environmental factors that could interfere with the process. This experiment was critical in establishing proof of concept for the nascent industry of quantum communications.