QUANTUM COMPUTING AND TECHNOLOGIES FOR THE FUTURE

We had mentioned earlier that quantum information is very different than classical information. We saw that while classical information is independent of its physical representation, quantum information cannot be read without disturbing the physical process encoding it. In addition, we mentioned that the Quantum No-Cloning Theorem prevents us from copying quantum information without errors.

However, there is a third difference between quantum and classical information that opens up incredible possibilities for the future. The concept is that all possible data that could be held by a quantum system are simultaneously contained by that quantum system. For example, one qubit simultaneously contains a digital “0” and a digital “1” in a superposition of states. Two qubits simultaneously hold “00”, “01”, “10,” and “11” in quantum superposition. As shown in Figure 157, the number of states allowed in the superposition grows exponentially with the number of available qubits. For an n-qubit register, the number of states in superposition is 2ⁿ. For a modest 500-qubit register, the number of states in superposition can be 2⁵⁰⁰, a number that vastly exceeds the number of atoms in the whole universe!

Figure 157 A classical 4-bit register can store only one of 16 different numbers from zero = 0000 to fifteen = 1111. It doesn’t matter what the method of representation—dead or live cats, ones or zeros, decimal numbers, or words—the classical information doesn’t change. On the contrary, a 4-qubit quantum register stores a superposition of all 16 different numbers at the same time. The coefficients a, b, c, … p are related to the probability of each state. In a quantum computer, all 16 states can be manipulated at once, allowing much faster calculation than with a classical computer.

As we saw in the analysis of teleportation, quantum states can be manipulated without destroying the quantum superposition, which makes it possible to compute with quantum information. The advantage of quantum computing over classical computing is that each calculation simultaneously evaluates all of the possibilities that can be encoded by the system. A single computational operation on a quantum system containing n qubits is the equivalent of performing 2ⁿ operations on a classical computer.

Let’s try to explain this difficult concept in a simpler way. As shown in Figure 157, let’s suppose that we have a 4-qubit register made of four Schrödinger’s cat boxes. If we finally open the boxes (we make a measurement), the register will indicate a certain 4-bit number in which each bit will be , . However, while the boxes are sealed, each cat is in a superposition of dead and alive states. As such, the register is in a superposition of all of its probable states:

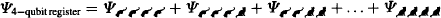
We could put this in a bra-ket notation:

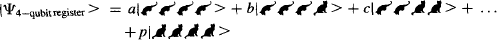
where the variables a, b, c, … p are related to the probability of each state. These numbers could be positive, negative, or complex, as long as the total probability adds up to one.

The power of a quantum computer is realized if we find a sequence of operations that can modify the quantum state (the value of the individual probabilities) without destroying the quantum superposition. Each operation modifies all of the quantum states at once, so a single quantum operation performs the equivalent of 2ⁿ classical operations. These operations are the quantum computer’s algorithm, and the result is obtained by finally making a measurement and collapsing the 4 qubits into 4 classical bits.

The power of a quantum computer scales exponentially as the number of qubits grows. For example, a modest quantum computer containing just 500 qubits would be able to perform in a single operation the gargantuan task of conducting 2⁵⁰⁰ classical operations—something that not even the largest classical, massively parallel super-computer can do today with a single operation!

All of this is largely theoretical at the moment. The hardware for making a quantum computer containing more than just a few qubits hasn’t been designed yet, and very few quantum algorithms have been invented. The whole field of quantum information is certainly in its earliest infancy. Hopefully, will inspire you to be one of the pioneers of the coming quantum information era.