General Properties of Saturated Oil
The bubble-point pressure is the important variable in characterizing saturated oil. At pressures above the bubble point, oil behaves like a liquid; below the bubble point, gas comes out of solution, becoming free gas coexisting with oil. The formation volume factor, Bo, measured in res bbl/STB, for oil above the bubble-point pressure includes all of the solution gas. At a pressure below the bubble point, the Bo refers to the liquid phase and its remaining dissolved gas at that pressure.
Figure B-1a in Appendix B shows a plot of Bo versus pressure for an example two-phase well. As oil is produced from a fixed reservoir volume, the reservoir pressure decreases. Above pb, Bo increases with decreasing pressure, reflecting the expansion of the undersaturated oil. This increase is slight because liquid oil compressibility is small. Below pb, Bo decreases as pressure decreases, reflecting the loss of gas from the oil and the resulting increase in the oil gravity.
In Figure B-1b the formation volume factor of the gas, Bg, increases nonlinearly with decreasing pressure because the gaseous phase is much more compressible than liquid oil, and this effect is more pronounced at lower pressure. Finally, Figure B-1c shows the solution gas–oil ratio, Rs. Above the bubble-point pressure, Rs is constant as Rsb, the solution gas-oil ratio at the bubble-point pressure, because the solution gas remains in the oil. Below the bubble-point pressure, Rs decreases with decreasing reservoir pressure because gas comes out of solution, leaving a decreasing amount of gas still dissolved in the oil. The solution gas–oil ratio is the amount of gas that would be liberated from a unit volume of oil at standard conditions.
When the produced gas–oil ratio observed for a well is greater than the solution gas–oil ratio, this signals that the reservoir pressure near the well is below the bubble-point pressure, and free gas that came out of solution will flow with the oil. The variables Bo, Bg, and Rs are related through the total formation volume factor, Bt, which accounts for both oil and free gas:

where Rsb – Rs is produced as free gas. If Bg is given in res ft3/SCF, then Bg must be divided by 5.615 to convert to res bbl/SCF. These pressure–volume–temperature (PVT) properties are usually obtained in the laboratory and are unique to a given reservoir fluid.
Example 3-1. PVT Properties Below the Bubble-Point Pressure: Impact on Oil Reserves
Calculate the total formation volume factor at 3000 psi for the reservoir fluid described in Appendix B. What would be the reduction in volume of oil (STB) in 4000 acres of the reservoir described in the same Appendix when the average pressure is reduced from the initial pressure to 3000 psi? Assume that the initial pressure is the bubble-point pressure and is equal to 4336 psi.
Solution
From the figures in Appendix B, Rsb = 800 SCF/STB, and at 3000 psi Bo = 1.33 res bbl/STB, Bg = 5.64 × 10–3 res ft3/SCF, Rs = 517 SCF/STB. Then from Equation (3-1),
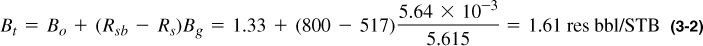
From Appendix B, Bob = 1.46 res bbl/STB, and from Equation (1-3), the original-oil-in-place at pi = pb is (from Figure B-1a)

For Bt = 1.61 res bbl/STB, N = 330 MMSTB, a reduction of 30 MMSTB. The remaining original reservoir volume is now filled with gas that came out of solution from the oil.
Figures 3-2 and 3-3, from Standing’s (1977) seminal work in oilfield hydrocarbon correlations, relate important variables such as Rs, γg, γo, T, pb, and Bo for a large number of hydrocarbons. These correlations should be used only in the absence of experimentally determined PVT properties obtained for the specific reservoir. The correlation shown in Figure 3-2 can be computed with the following equation:
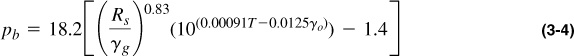
with T in °F and γo in °API.
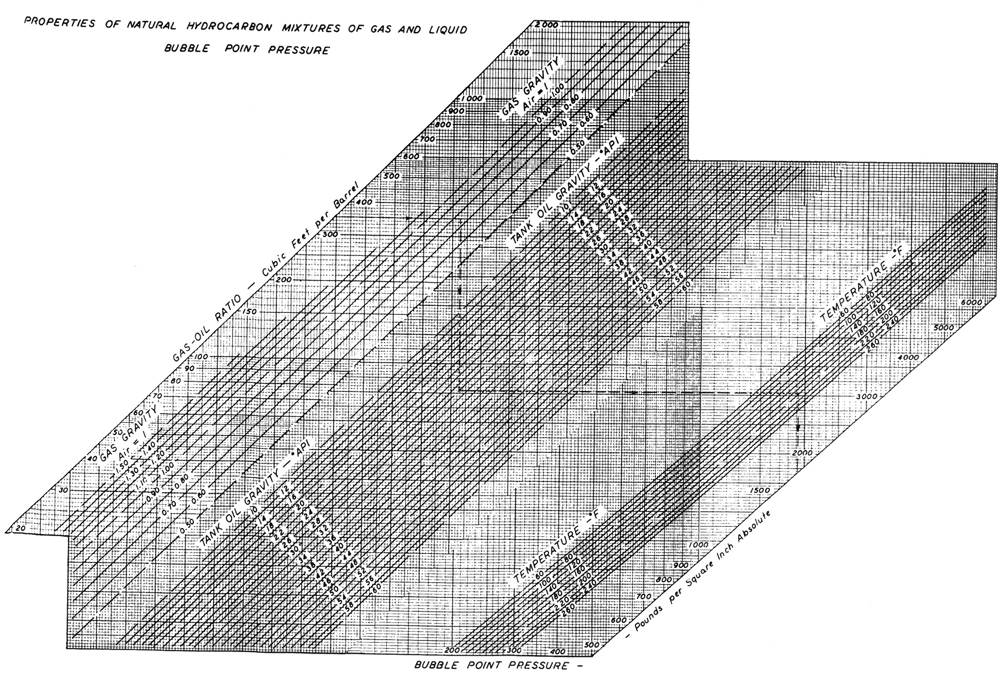
Figure 3-2. Properties of natural mixtures of hydrocarbon gas and liquids, bubble-point pressure. (After Standing, 1977.)
Example 3-2. Use of Correlations to Obtain PVT Properties of Saturated Oil Reservoirs
Supposing that Rs = 500 SCF/STB, γg = 0.7, γo = 28°API, and T = 160°F, calculate the bubble-point pressure. What would be the impact if Rs = 1000 SCF/STB but all other variables remain the same?
If Rs = 500 SCF/STB, Bob = 1.2 res bbl/STB, T = 180°F, and γo = 32°API, what should be the gas gravity, γg?
Solution
Reading from Figure 3-2 in a stairstep manner with the first set of variables, pb = 2650 psi. If Rs = 1000 SCF/STB, then pb = 4650 psi. Using Equation (3-4),

For Rs = 1000 SCF/STB, pb = 4698 psi, Figure 3-3 can be used for the last question. Stating from the right at Bob = 1.2 res bbl/STB, T = 180°F, and γo = 32°API and then from the left at Rs = 500 SCF/STB, the intersection of the two lines results in γg = 0.7.
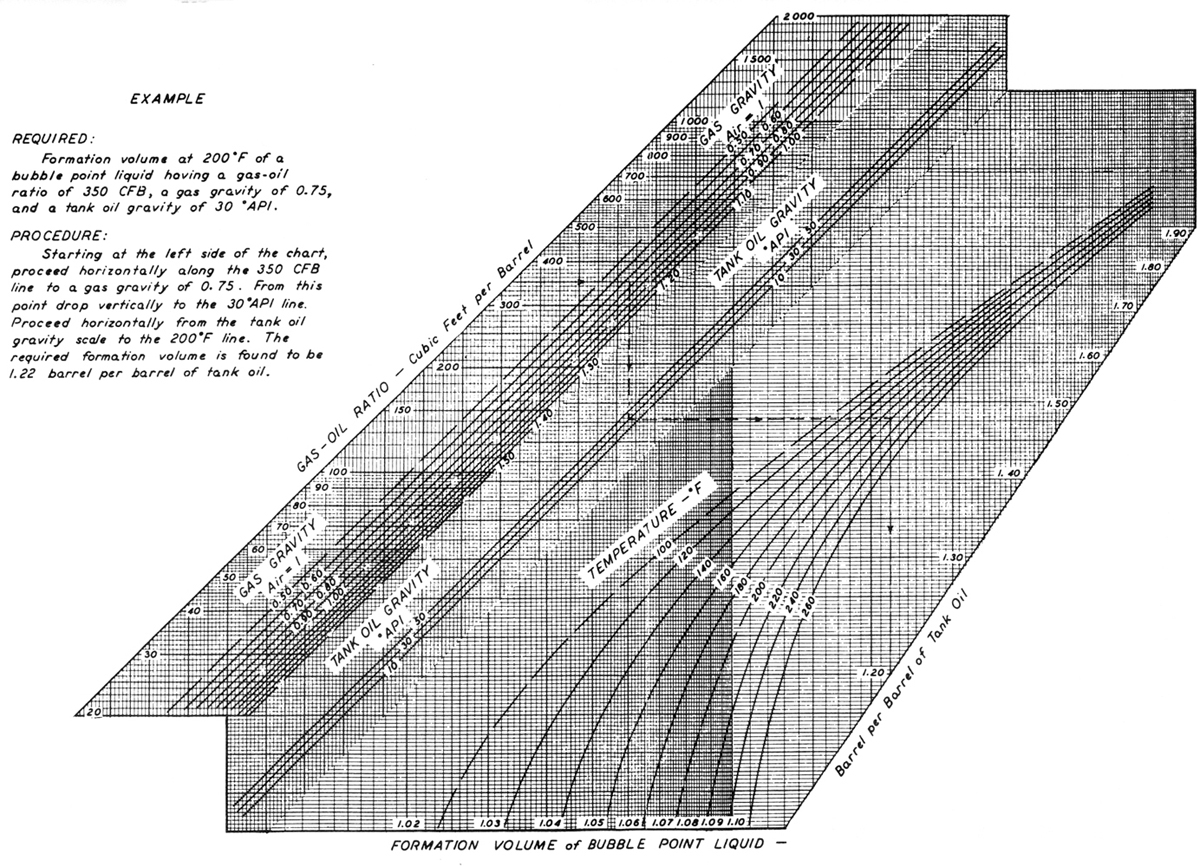
Figure 3-3. Properties of natural mixtures of hydrocarbon gas and liquids, formation volume of bubble-point liquids. (After Standing, 1977.)
Leave a Reply