Many practical problems involve permutations and combinations of objects. A first question is: Given a collection of n objects, in how many ways can we permute them? For instance, let us consider the set {a, b, c}. Since the set is quite small, we can enumerate all of the possible permutations systematically. First we consider permutations beginning with a; we can form two such permutations, (a, b, c) and (a, c, b). Then, considering permutations starting with b, we have (b, a, c) and (b, c, a), and by the same token we have (c, a, b) and (c, b, a), beginning with c. Hence, there are six possible permutations of three objects, but what can we say in general for n objects? Again, let us be systematic in our enumeration of permutations:
- When we choose the first item in the sequence, we have n possibilities.
- When we choose the second item, we have n − 1 possibilities, since one object has already been used to fill the first slot.
- When we choose the third item, we have n − 2 possibilities, since two objects have already been used to fill the first and second slots.
- When we have only two items to go, we can choose among two.
- When we have one item left, there is just one possible choice.
Hence, the total number of permutations of n objects is
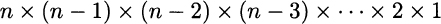
The kind of product above is so common that it has been given a name.
DEFINITION 2.1 (Factorial) Given a positive integer number n, the factorial of n, denoted by n! is defined as
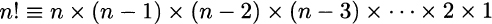
The factorial can also be defined recursively as
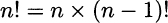
and, by convention, we set 0! = 1.
A noteworthy feature of the factorial function is that it grows very quickly with n:
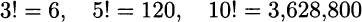
This process is known as combinatorial explosion and has practical implications.
Example 2.1 Imagine that you are a traveling salesperson. You live in a city, and your task is to visit customers living in other cities and then come back home. Let n be the number of cities you have to visit, not including yours; all of them must be visited exactly once. Arguably, you would like to follow the shortest route in your tour. Geographic information systems can provide you with distances dij between any pair of cities (i, j), where i ≠ j and the indices range over the set {0, 1, 2, …, n} (say that 0 is your city). How can we find the optimal tour?
One obvious idea is that, since there must be a finite number of tours, we could just enumerate all of them and pick up the shortest one. Using a fast computer, this should be no big deal. But how many tours must be evaluated? We have n + 1 cities to visit. There are (n + 1)! permutations of them, but actually only n! are really different. One way of seeing this is observing that the first city is your home and is fixed. An alternative view is that we do have (n + 1)! different tours, since there are n +1 possible starting points, but the total length is not really influenced by the starting city as the tour is a closed cycle; hence, the number of different tours in term of total length is (n + 1)!/(n + 1) = n!. The problem is further simplified if we assume symmetric distances, i.e., dij = dji. In fact, there is little difference in terms of mileage between traveling from Boston to New York or from New York to Boston. This may not apply on a smaller scale: Within a city, one-way streets make distances asymmetric. If we assume symmetry, we have two equivalent ways of traveling along each tour; you may visualize them as a clockwise and a counterclockwise tour. Hence, the total number of different tours is n!/2.
Now, say that you have to visit 25 customers. Using any pocket calculator, we obtain
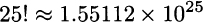
Some difficult number to read! It means that there are about 15.5112 millions of billions of billions of possible permutations of 25 cities. Luckily, we must only consider half of those, and we also have a very fast computer. Say that we are able to generate and evaluate one billion permutations, i.e., 109, per second. Since there are 3600 seconds per hour, 24 hours per day, and 365 days per year, we will get the optimal tour after
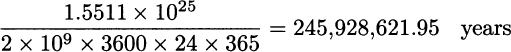
Patience is indeed a virtue, but you need a solution, not your (many times grand)-nephews; luckily there are much smarter ways to find the optimal solution, using some good mathematics.
Now let us consider a slightly different combinatorial problem. We have n items, and we want to select a combination of r of them. To see a practical setting in which a combination of items must be selected, imagine a batch of n manufactured parts, from which a random sample of r items is drawn for a quality check. How many combinations of r items out of n can we form? One way to look at the task is the following:
- We take any permutation of n items, and we know that there are n! possible permutations.
- Then we select the first r items and we include them into our combination, leaving the remaining n − r items outside. However, we are not really interested in the order of the r items; all of their r! permutations correspond to the same combination, and the same applies for the (n − r)! permutations of the objects that we do not include in the combination.
Hence, there are
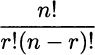
combinations of r items out of n. As this quantity is quite common, too, it has earned a specific name.
DEFINITION 2.2 (Binomial coefficient) Given positive integer numbers n and r, r < n, the binomial coefficient is defined as
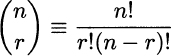
Example 2.2 Consider n = 4 objects. How many combinations of two items can we form? Using binomial coefficients, we find
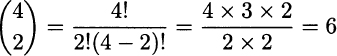
Indeed, in soccer championships groups of four teams are formed and six matches between all of them played. Note that in this case the order of the two teams in defining a match is inconsequential, as there are no return matches.
To see where the name “binomial” comes from, we recall the binomial expansion formula:
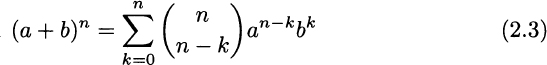
Example 2.3 We all remember the following formulae from high school math:
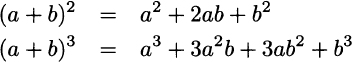
Let us work them out using the binomial expansion formula. For the first case we have
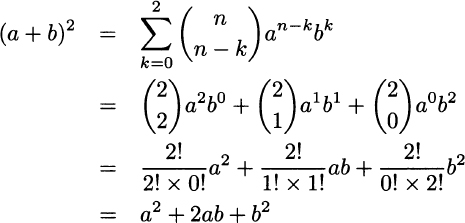
where we see the usefulness of setting 0! = 1 in Definition 2.1. The second case is also easy to check, by observing that
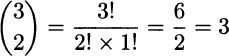
In practice, when computing a binomial coefficient, care must be taken as large numbers can result in overflow errors on a computer.5 A good way to simplify the calculation is to note that
Leave a Reply