Consider two or more beds of equal cross section but of unequal lengths and permeabilities (Fig. 8.7, depicting flow in series) in which the same linear flow rate q exists, assuming an incompressible fluid. Obviously the pressure drops are additive, and
(p1 – p4) = (p1 – p2) + (p2 – p3) + (p3 – p4)
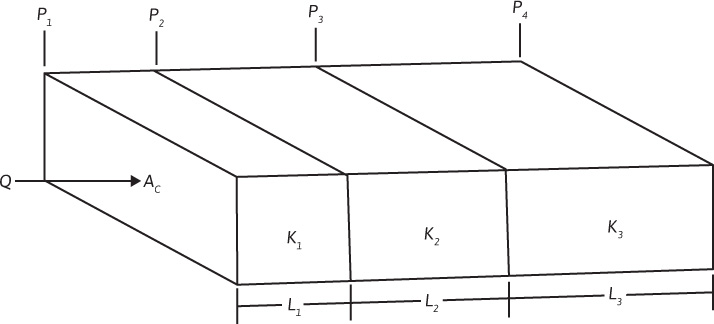
Figure 8.7 Series flow in linear beds.
Substituting the equivalents of these pressure drops from Eq. (8.7),
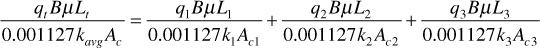
But since the flow rates, cross sections, viscosities, and formation volume factors (neglecting the change with pressure) are equal in all beds,
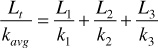
or
The average permeability as defined by Eq. (8.14) is that permeability to which a number of beds of various geometries and permeabilities could be approximated by and yield the same total flow rate under the same applied pressure drop.
Equation (8.14) was derived using the incompressible fluid equation. Because the permeability is a property of the rock and not of the fluids flowing through it, except for gases at low pressure, the average permeability must be equally applicable to gases. This requirement may be demonstrated by observing that, for pressures below 1500 psia to 2000 psia,
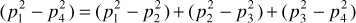
Substituting the equivalents from Eq. (8.10), the same Eq. (8.14) is obtained.
The average permeability of 10 md, 50 md, and 1000 md beds (which are 6 ft, 18 ft, and 40 ft in length, respectively, but of equal cross section) when placed in series is
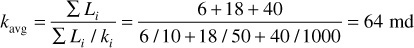
Consider two or more beds of equal length but unequal cross sections and permeabilities flowing the same fluid in linear flow under the same pressure drop (p1 to p2), as shown in Fig. 8.8, depicting parallel flow. Obviously the total flow is the sum of the individual flows, or
qt = q1 + q2 + q3
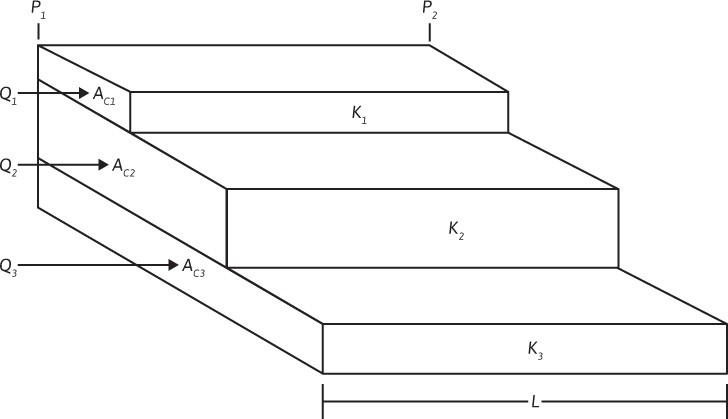
Figure 8.8 Parallel flow in linear beds.
and
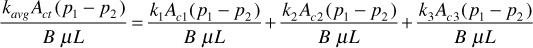
canceling
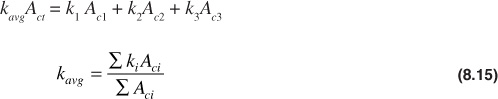
And where all beds are of the same width, so that their areas are proportional to their thicknesses,

Where the parallel beds are homogeneous in permeability and fluid content, the pressure and the pressure gradient are the same in all beds at equal distances. Thus there will be no cross flow between beds, owing to fluid pressure differences. However, when water displaces oil—for example from a set of parallel beds—the rates of advance of the flood fronts will be greater in the more permeable beds. Because the mobility of the oil (ko/μo) ahead of the flood front is different from the mobility of water (kw/μw) behind the flood front, the pressure gradients will be different. In this instance, there will be pressure differences between two points at the same distance through the rock, and cross flow will take place between the beds if they are not separated by impermeable barriers. Under these circumstances, Eqs. (8.15) and (8.16) are not strictly applicable, and the average permeability changes with the stage of displacement. Water may also move from the more permeable to the less permeable beds by capillary action, which further complicates the study of parallel flow.
The average permeability of three beds of 10 md, 50 md, and 1000 md and 6 ft, 18 ft, and 36 ft, respectively, in thickness but of equal width, when placed in parallel is
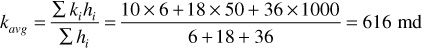
Leave a Reply