As mentioned in Section 3.10, the ideal gas law is extremely important to air pollution engineers. Compliance with federal and state laws requires not only proper environmental engineering design and operation of pollution abatement equipment but also careful analysis and accurate measurements of specified pollutants and environmental quality parameters. In the design process and in other types of calculations, engineers who have complete understanding of the ideal gas law will achieve greater accuracy with a smaller expenditure of their time. In this section, through the USE of example problems, we will review various uses of the ideal gas law.
Emission sampling is another important area for which a good understanding of the ideal gas law and the equipment used to measure gas flow is important. Many poorly performing systems are results not of bad design practice but of poor sampling techniques.
Some important considerations in gas sampling are equipment calibration, leaks, sample handling (condensation, adsorption), process operation fluctuations, and representative sampling of the process stream. We will address some of these considerations in the following examples.
When Eq. (3.5) was first presented, one widely used value of R was given for a specific set of units. There are many numerical values of R depending on the units chosen for P, T, V, and n. Table C.3 provides a list of several possible values of R, and the derivation of one such value is illustrated in Example 3.8.
EXAMPLE 3.8
Given that the molar volume of an ideal gas is 22.4136 l/gmol at 273.15 K and 1.000 atm, calculate the value of R in units of mm Hg‐ft3/lbmol‐R.
SOLUTION

In this example problem, more significant figures were used than are typically used in engineering calculations. Engineers often are satisfied with only three‐ or four‐digit significance. Indeed, the data derived from field measurements are often accurate only to two significant figures. In an age of pocket calculators and personal computers, when it has become routine to obtain numerical answers to eight decimal places, it is important to understand the significance of the numbers we work with. When high accuracy and precision are needed and justified, then many significant figures should be used. However, in many design problems the equations are modified by empirical relationships and must be considered to be approximate.
The weighted‐average molecular weight of a mixture of ideal gases is calculated using mole fractions or volume fractions (not mass fractions) as the weighting factors. This is demonstrated in the following example problem.
EXAMPLE 3.9
Dry air can be considered to be 78.0% nitrogen (M.W. = 28.0), 21.0% oxygen (M.W. = 32.0), and 1.0% argon (M.W. = 40.0). Calculate the average molecular weight of air.
SOLUTION
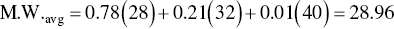
The density of an ideal gas mixture is a molar average of the densities of the pure components. The density can also be calculated by using the molar‐average molecular weight of the gas mixture in Eq. (3.8), as shown in the next example. Note that the density of a gas depends on the pressure and temperature.
EXAMPLE 3.10
Calculate the density of air at standard conditions (T = 25 °C and P = 1 atm).
SOLUTION
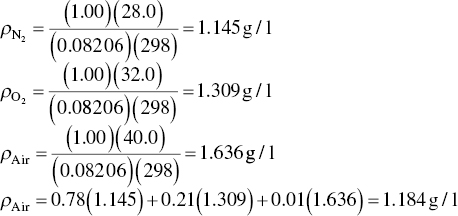
Alternatively,
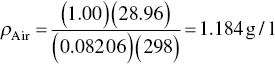
Leave a Reply