In spite of its success with explaining the spectral lines produced by the hydrogen atom, Bohr’s atomic model is not perfect. It only works for atoms that have one electron. That is, it only applies to hydrogen, ionized helium (He+), doubly ionized lithium (Li++), and a few other light ions. More importantly, however, it does not justify Bohr’s assumption that electrons moving in circular orbits would not lose energy by radiation. It would take a decade before French physicist Louis de Broglie could explain the lack of radiation by proposing that the electron is not a classical particle traveling through an actual circular path. Today, we talk about the probability of an electron being in an orbital, rather than of an electron flying through space in an orbit.
Nevertheless, Bohr’s basic concept remains valid. Atoms indeed radiate photons when electrons jump between an allowed higher energy level (Figure 84a) to a lower allowed energy level (Figure 84b). This is the basis for most of our modern solid-state electronics. For example, LEDs—those ubiquitous little indicator lights in all of our modern appliances—emit light because electrons in the atoms of their active materials jump from a higher energy level to a lower energy level. LEDs emit light of a very specific color that depends on the electron energy levels allowed by the atoms in the active material. One needs to supply the same amount of energy to the atom so the electron will jump from the lower energy level to the higher energy level.
Figure 84 An atom in the excited state (a) decays to a stable “ground” level (b) by radiating energy. The absorption and radiation of energy takes place only in integer multiples of a fundamental unit of energy E, proportional through Planck’s constant h to the photon’s frequency f: E = hf. (c) A simple setup can be used to estimate Planck’s constant h from the operating threshold of a number of LEDs that emit light at different wavelengths λ. (d) The slope of a linear fit of the data yields a rough estimate of h/e.
A nice experimental proof of this is to determine Planck’s constant h with some inexpensive LEDs of different colors§ wired as shown in Figure 84c. At the very threshold for light emission, the voltage VLED across the LED is just enough to provide energy to the electrons to jump between two energy levels. Therefore:
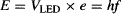
where e is the electron charge (e = 1.60 × 10−19 Coulomb). To conduct the experiment, you will need to measure the voltage across each LED when light emission just starts, so do this in a darkened room. By the way, the emission from the IR LED is invisible to the human eye, but digital cameras and video cameras (especially those with “night-vision mode”) are sensitive to IR, allowing you to see the IR LED light.
Once you have data for a number of LEDs, graph VLED against f. If you can’t find the LED’s specs for the exact wavelength of the light emitted, use the values shown in Table 2. The slope of the graph you just created is equal to h/e, allowing you to roughly estimate the value of Planck’s constant h. For reference, the recognized value for Planck’s constant is h = 6.626 × 10−34 J · s.
Because of the dependence of the eye’s threshold on color, and due to real-world properties of LEDs, this method of determining Planck’s constant is not precise at all. However, it should give you a nice, instinctive feel for the dependence of photon energy (represented by its color) and the electron jump necessary to emit the photon.
Leave a Reply