One-tail tests

When the null hypothesis is of the form H₀ : μ = μ₀, we consider a two-tail rejection region. In many problems, the null hypotheses has the form H₀ : μ ≥ μ₀ or H₀ : μ ≤ μ₀ are more appropriate. As one could expect, this leads to a rejection region consisting of one tail. Before illustrating the technicalities involved, it is useful to consider a practical example.

Example 9.14 A firm manufactures a product whose average useful life is 1250 hours. This average comes from an extended experience in the past, and it can be considered as a very reliable estimate of the expected value of life. The firm is currently engaged in a product improvement program, based on a different manufacturing process. A sample of 30 items produced by this new process is tested, resulting in a sample mean of 1315 hours and a sample standard deviation of 70 hours. Can we say that the new process is really better than the old one?

This is a typical case lending itself to hypothesis testing, but here we are not interested in a two-tail test. What we would like to check is whether the difference between 1315 and 1250 hours is statistically significant and cannot be attributed to a lucky sample. In other words, we would like to reject the hypothesis that the expected life is still 1250, but we certainly would not be happy if the sample mean were less than that, as this would not support the claim that the firm did a good job. The correct way to state the problem, from the point of view of the firm itself, requires the null hypothesis

against the alternative:

The firm would like to prove that the product has really been improved, but we should not state a null hypothesis like H₀ : μ ≥ 1250. This is quite tempting, and in fact many students fall into this trap and make different sorts of mistakes:

• Some go as far as to state hypotheses involving the sample mean 1315, which makes no sense since this is a sample statistic, not an expected value.
• Moreover, we should not run a two-tail test, as we would also reject the null hypothesis when the sample mean is 1000 hours, which does not really suggest that the product has been improved.
• Finally, a null hypothesis like H₀ : μ ≥ 1250 is true regardless of whether they improved the product (average life is larger than 1250) or not (average life is still 1250); hence, a test of such a hypothesis does not discriminate between the alternatives that we are interested in comparing.

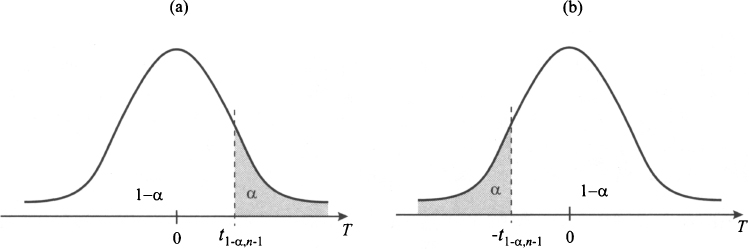
Fig. 9.5 Rejection regions for one-tail hypothesis testing.

We should keep in mind that, with standard test procedures, we can either reject or fail to reject. We do not really prove that a claim is true; we may just argue that there is strong evidence against a claim. So, if we want to support a statement, we should try to reject its negation. This is why, in this problem, the claim that the firm would like to prove plays the role of the alternative hypothesis (9.14).

What kind of rejection region should be associated with the test in the example? The reasoning is almost the same as in two-tail testing, but it is easy to see that we should reject the null hypothesis if the test statistic TS is large, as this supports the one-sided alternative. If the test statistic is large, this means that the average life we observe is much larger than μ₀, and it is hard to explain this discrepancy by sampling variability alone. Indeed, the rejection region is the right tail, as shown in Fig. 9.5(a). Formally, the test should be run as follows:

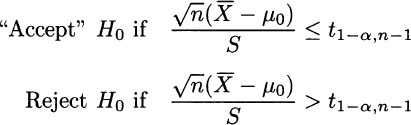
Note that here we should use a quantile with probability level (1 − α) instead of (1 − α/2). In this case, the rejection region consists of one tail, and the probability of a type I error is not split in two. In Example 9.14, the test statistic is

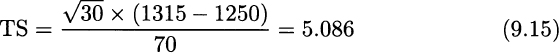
The sample size is 30, so we are not really allowed to use quantiles from the standard normal distribution, but we are close; by remembering the ±3σ rule, we see that the null hypothesis will be rejected for any sensible significance level when the test statistic is larger than 3, when using quantiles of the standard normal. If we insist in using the t distribution, say, with α = 0.5%, which is pretty small, the correct quantile is t_0.995,29 = 2.756 < TS. So we see that we reject even if we require a very small probability of type I error.

To complete the picture, let us consider the case of

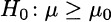
against the alternative

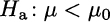
Here, the rejection region is the left tail [see Fig. 9.5(b)]

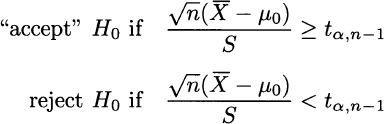
The quantile t_α, n−1, with a sensibly small significance level (α < 50%), is actually negative. Given the symmetry of the t distribution, t_{α, n−1} = −t_{1−α, n−1}, and the rejection region is also characterized by the condition

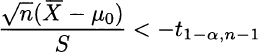
Before we proceed further, we should insist again that, strictly speaking, what we have said so far applies only to the expected value of a normal distribution. If the sample is normal, then we can say that the TS statistic has t distribution. In other cases, we have to carefully examine the distribution of the test statistic that we are considering, in order to properly set up the test; yet, the kind of reasoning is the same. It is also important to see the role of the two hypotheses in setting up the test:

• The alternative hypothesis determines the rejection region, which in the case we consider here might be the right tail, the left tail, or both. If the test statistic falls in one of these “extreme” regions, there is strong evidence against the null hypothesis.
• The null hypothesis specifies the probability distribution of the test statistic. In this simple setting, the null hypothesis just specifies the expected value μ₀. This is not so obvious for one-tail tests: If the null hypothesis is H₀ : μ ≤ μ₀, why should we just consider μ₀ and not any smaller value, that would be compatible with the null hypothesis anyway? To see a heuristic justification, we should keep in mind the conservative nature of hypothesis testing. If TS falls in the rejection region assuming that μ = μ₀, i.e., ifthen it will also fall in the rejection region for any assumed value less than μ₀. By assuming μ = μ₀, we take the worst case from the point of view of the alternative hypothesis; this approach is consistent with the idea of keeping the probability of a type I error small. In Section 9.10 we offer a more rigorous look at hypothesis testing.

As a final observation, we have illustrated testing procedures for the mean of a normal population, when standard deviation σ is not known and must be estimated by its sample counterpart S. This is the standard case in business applications, but if σ were known, it would be easy to adapt the approach. We should just consider a test statistic , which is standard normal, and apply the procedures described above using quantiles of the standard normal distribution.