Newtonian and Non-Newtonian Fluids

An ideal fluid has zero viscosity. Shear force is not involved in its deformation. An ideal fluid must be incompressible. Shear stress is zero irrespective of the value of ∂u/∂y. Bernoulli equation can be used to analyse the flow. Real fluids having viscosity are divided into two categories, namely, Newtonian and non-Newtonian fluids. In Newtonian fluids a linear relationship exists between the magnitude of the applied shear stress and the resulting rate of deformation. It means that the proportionality parameter, μ is constant in the case of Newtonian fluids. The viscosity at any given temperature and pressure is constant for a Newtonian fluid and is independent of the rate of deformation. The characteristics are plotted in Figure 9.2.

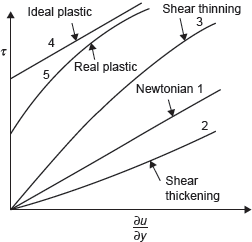
Figure 9.2 Type of Fluids

Non-Newtonian fluids can be further classified as simple non-Newtonian, ideal plastic, and shear thinning, shear thickening, and real plastic fluids. In non-Newtonian fluids, viscosity varies with variation in the rate of deformation. Linear relationship between shear stress and rate of deformation (∂u/∂y) does not exist. In plastics, up to a certain value of applied shear stress there is no flow. After this limit, it has a constant viscosity at any given temperature. In shear thickening materials, the viscosity increases with (∂u/∂y) deformation rate. In shear thinning, materials viscosity decreases with (∂u/∂y).