In mechanistic models, it is assumed that a certain number of reactions, events, or “hits” (concept derived from radiation biology), or transition stages, related to a critical target in the cell (DNA), are necessary to transform a normal cell to a cancer cell. These models are important because there seems to be general consensus that tolerance distribution models (e.g. Mantel–Bryan) should not be used unless the available data are accurate enough to exclude models involving a linear component in the low‐dose region, or a genotoxic mechanism might be involved.
The multistage model, first proposed by Armitage and Doll (1954), is an extension of the one‐hit model developed for ionizing radiations. One generalized version of this model where at least one of the stages is assumed to be dose‐related takes the form:
(5.1)![]()
where
- P(D) = the probability of cancer at dose D
- qk = coefficients to best fit to the data
- Dk = applied does raised to the kth power
- k = number of stages (usually set arbitrarily at the number of dose levels minus one.
The most likely estimate at very low does becomes increasingly unstable with a small change in the response at experimental does. Therefore, a further development in modeling was the replacement of the linear term in the polynomial function by its 95% confidence limit to achieve more stable estimates of risk above background than are obtained for the most likely estimates. This so‐called linearized multistage model is used routinely by the Environmental Protection Agency (EPA) and has, therefore, become the most widely used model for estimation of cancer risk. At low doses, the function becomes essentially linear. The multistage model is very flexible in fitting data sets because it is a polynomial function of dose. The so‐called carcinogen potency factors provided by the EPA have been based on this model and are calculated from animal data using commercially available computer programs.
The multistage model is favored by the EPA because it generally gives conservative risk estimates for low exposures, but the model has several weaknesses.
As an example, pica is a real phenomenon and should be considered, but the assumption that toddlers who eat 200 mg/day of soil will continue this behavior for a 70‐year lifetime is not realistic. Thus, the impact of assumptions on the exposure point concentration and, ultimately, the risk values should be examined to identify which of the myriad of input variables have the most significant impact on the resulting risk value. Such a refinement is called a sensitivity analysis.
Receptor Doses
The final step in the exposure assessment stage is to estimate the doses of the different classes of chemicals to which receptors are potentially exposed at the exposure points. There are three types of dose: the administered dose (the amount ingested, inhaled, or in contact with the skin), the intake dose (the amount absorbed by the body), and the target dose (the amount reaching the target organ).
For purposes of calculating risks, the dose should be in the same form as that of the dose–response relationship reported for the specific chemical and the exposure route under study. This will almost always be either administered dose or absorbed dose. Given the concentration of the contaminant at the exposure point, the calculation of administered dose is straightforward. In contrast, the calculation of absorbed dose based on administered dose requires consideration of some complex factors. The key factors influencing the uptake of contaminants by the body are simplified as follows:
| Ingestion | Contaminant concentration in the ingested medial |
| Amount of ingested material | |
| Bioavailability to the gastrointestinal system | |
| Inhalation | Concentration in air and dust |
| Particle size distribution | |
| Bioavailability to the pulmonary system | |
| Rate of respiration | |
| Dermal contact | Concentration in soil and dust |
| Rate of deposition of dust from air | |
| Direct contact with soil | |
| Bioavailability | |
| Amount of skin exposed |
Other factors to be considered in determining the intake of contaminants include considerations of life style, frequency and duration of exposure (e.g. chronic, subchronic, or acute), and the body weight of the receptor. In the majority of hazardous waste sites, long‐term (i.e. chronic) exposures are frequently of greatest concern.
The calculation of an administered dose is summarized in the following generic equation:
where
- I = intake (mg/kg of body weight‐day)
- C = concentration at exposure point (e.g. mg/l in water or mg/m3 in air)
- CR = contact rate (e.g. l/day or mg/m3/day)
- EF = frequency (day/year)
- ED = exposure duration (year)
- BW = body weight (kg)
- AT = averaging time (days)
Equation (5.2) is typical modified for specific exposure pathways. For example, the intake dose from the inhalation of fugitive dust may be calculated as
(5.3)![]()
where
- RR = retention rate (decimal traction)
- ABS = absorption into bloodstream (decimal fraction)
For fugitive dust, the concentration in the air is determined by
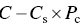
where
- Cs = concentration of chemical in fugitive dust (mg/mg)
- Pc = concentration of fugitive dust in air (mg/m3)
Often, appropriate parameters may be found in the literature. Considerable research has been done in recent years to define many basic parameters, such as skin surface areas, soil ingestion rates, and inhalation rates. Other parameters, such as exposure frequency and duration, are often based on site‐specific information (if available) or professional judgment. For example, in the evaluation of a trespasser scenario, observations of trespassers during site investigation activities may dictate the values used for exposure frequency (e.g. number of days per year or number of events per year) and exposure duration (e.g. number of years that the activity occurred). Common sense also plays an important role in the selection of exposure parameters. For example, if one were evaluating residential use of two sites, one in North Dakota and one in Florida, it would not be reasonable to assume the exposure frequency (e.g. days per year that an activity occurred) would be the same in the two risk assessments for a child potentially exposed to surface soils as a result of playing in the backyard.
Averaging time (AT) is another important parameter which must be defined in the intake equation. The averaging time selected will depend on the type of constituent being evaluated. For example, to assess long‐term or chronic effects associated with exposure to noncarcinogens, the intake is averaged over the exposure duration (expressed in days). Exposure to carcinogens, however, is averaged over a lifetime (assumed to be 70 years or 25 550 days), to be consistent with the approach used to develop slope factors.
Some parameters used for this type of calculation are shown in Table 5.3. It should be noted that these values can vary greatly depending on the assumed exposure conditions (i.e. the selected exposure scenario). As an example, the air‐breathing rate for adult males is 0.83 m3/h in Table 5.3. However, this rate can vary by an order of magnitude from 0.6 m3/h at rest to 7.1 m3/h for vigorous physical exercise.
Table 5.3 Standard parameters for calculation of dosage and intake determined for a landfill.
| Parameter | Adults (males) | Child age 6–12 | Child age 2–6 |
| Average body weight (kg) | 70 | 29 | 16 |
| Skin surface area (cm2) | 18 150 | 10 470 | 6 980 |
| Water ingested (l/day) | 2 | 2 | 1 |
| Air breathed (m3/h) | 0.83 | 0.46 | 0.25 |
| Retention rate (inhaled air) (%) | 100 | 100 | 100 |
| Absorption rate (inhaled air) (%) | 100 | 100 | 100 |
| Soil ingested (mg/day) | 100 | 100 | 200 |
| Bathing duration (minutes) | 30 | 30 | 30 |
| Exposure frequency (days) | 365 | 365 | 365 |
| Exposure duration (years) | 30 | 6 | 4 |
Examples 5.5 and 5.6 illustrate the calculation of contaminant intake via the inhalation and dermal route, respectively.
EXAMPLE 5.5 CALCULATION OF CONTAMINANT INTAKE
Determine the chronic daily inhalation intake, by adults, of a noncarcinogenic chemical as a function of concentration in fugitive dust at the ABC Landfill (Table 5.3).
SOLUTION
For an adult exposed to a noncarcinogenic constituent, the intake IN may be calculated from Eq. (5.2):
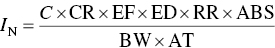
From Table 5.3, we take the air‐breathing rate for adults as 0.83 m3/h and write
- CR = 0.83 × 24 = 19.92 m3/day
- EF = 365 days
- ED = 30 years for chronic exposure to noncarcinogens
In the absence of better information, a conservative approach would assume the RR and the absorption into bloodstream would both equal 1.0.
- BW = 70 kg (Table 5.3)
- AT = 365 days × 30 years


- C = exposure point concentration (mg/m3)
EXAMPLE 5.6 AVERAGE DAILY INTAKE FROM DERMAL CONTACT WITH SOIL
Determine the average daily intake of chlorobenzene over one year of exposure for on‐site workers from dermal contact of the soils:
Assume the following additional parameters:
- A = skin exposed = 20% − 0.2 × 18150 cm2 – 3630 cm2
- DA = dust adherence − 0.51 mg/cm2
- ABS = skin absorption rate − 6%
- SM = effect of soil matrix = 15% (i.e. due to soil matrix only 15% of contamination is actually available for contact)
- EF = two exposure events per day; 156 exposure days per year
- ED = 1 year
- BW = 70 kg
- AT = 365 days
SOLUTION
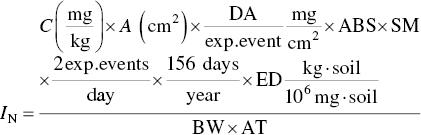
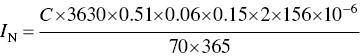
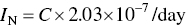
The given average concentration of chlorobenzene in soil is 1.39 mg/kg. The daily intake of chlorobenzene is
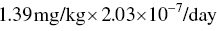
Thus,
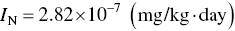
Again, the foregoing examples represent only two approaches to calculating contaminant intake in the course of an exposure assessment. The next factor to be analyzed is toxicity.
Leave a Reply