It is possible to use a modern CRT to measure e/m using Thomson’s method. However, it isn’t an easy task, because the deflection plates are relatively small, and their position is not well known due to the graphite coating used to reduce charge accumulation beyond the neck of the CRT. For this reason, specialized CRTs are made by didactic equipment companies to enable students to reproduce Thomson’s third experiment. One such tube sometimes found in the surplus market for around $150 is the model TEL-525 made by Tel Atomic.§§
However, the same inexpensive 2AP1 CRT that we used in our oscilloscope can be used to measure e/m using a modification of Thomson’s method developed by J. B. Hoag15,16 in the 1920s. As shown in Figure 51, the idea is to place the CRT within a solenoid while connecting an AC voltage across one set of deflector plates. The AC signal produces a line on the face of the CRT. As the current increases through the solenoid, this line appears to rotate and shorten because of an effect known as magnetic focusing. An analysis of this effect is beyond the scope but can be found in Hoag’s original.
Figure 51 This simplified diagram shows how you can use your CRT to measure e/m using Hoag’s method. An AC signal is placed across one set of plates of the CRT to produce a line on the screen. The solenoid is then energized until the line makes one complete helical turn. You can calculate e/m = 8π2V /B2 L2 using the accelerating voltage V between the cathode and the anode, as well as the magnetic field B needed to cause one complete turn of the line on the screen until it disappears into a small point. For the sake of clarity, we show a short solenoid. However, the solenoid should extend well past both ends of the CRT to ensure a homogeneous magnetic field.
At some point, the line would have made a whole turn and shrunk to a point. Just a small spot will appear on the screen. e/m can then be calculated from the magnetic field B needed to cause the line to rotate one full turn until it disappears into a point:
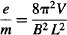
where V is the accelerating potential (voltage between anode and cathode of CRT) and L is the length of the helical path (distance between deflector plates and CRT screen).
The actual circuit for our setup is shown in Figure 52. We gutted a surplus power supply that we bought from Surplus Sales of Nebraska and used its original transformer and chassis. The specific transformer is not critical. Just use any transformer with ~150 VAC and 6.3 VAC secondaries. The only thing that you must check is that the transformer’s insulation is rated at 1,000 V or higher. Another possibility is to use a 6.3 VAC “filament” transformer and a separate 110 VAC/110 VAC isolation transformer (e.g., Magnetek N-48X). The over-100 VAC transformer is used to oscillate the electrostatic deflection plates, so selecting a specific voltage is not important.
Figure 52 We built this setup to measure e/m using Hoag’s method. (a) Schematic diagram of the circuit to energize the CRT and coaxial solenoid. High voltage is obtained from an external power supply. (b) A view of our setup ready to perform an experiment.
The accelerating voltage is obtained from an external high-voltage power supply. Either one of the high-voltage power supplies that we built in (Figure 31 or Figure 32) works well. This power supply is not connected directly to the cathode (because the intensity grid electrode must be more negative than the cathode), so a digital multimeter must be connected between the cathode and the anode to measure the accelerating potential V.
The solenoid coil is made of 16 AWG enameled magnet wire. Ideally, the coil should extend past the ends of the CRT by at least 5 cm, so you could wind a coil that is at least 30-cm-long. A 34-cm-long piece of 2-in. ID PVC pipe is a good center form for the solenoid. Wind five smooth layers of the magnet wire, making sure that you count the total number of turns that you wind on the solenoid. Our solenoid has over 1,100 turns.
We have a Gaussmeter available (an instrument to measure magnetic field), so we were able to find out quite precisely that the field produced by our solenoid is given by B[Tesla] = 0.004187 × Current[A]. However, the reason why we asked you to count the number of turns on your solenoid is because you can calculate the magnetic field B inside your solenoid as you energize it with current I if you know the total number of turns in your coil and the length Lsolenoid they occupy:
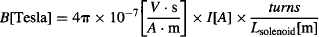
To conduct an experiment, you would set the accelerating voltage of the tube to an initial value V = 300 V. Set the controls to produce a thin vertical line. Start increasing the current through the solenoid until a full turn is traced by the line on the CRT. Record the accelerating potential and current through the solenoid. Repeat at various accelerating potentials (e.g., taking steps of 100 V up to a maximum of 800 V).
You will need to know the length L of the helical path. This is the distance between the center of the deflection plates and the screen. However, the graphite coating inside the tube will prevent you from measuring this directly, so we took an X-ray of the 2AP1 tube and found out these distances to be approximately 8.5 cm for one set of deflection plates, and 7 cm for the other set of plates (Figure 53).¶¶ You may use the same value if you are using a 2AP1 CRT.
Figure 53 X-ray of the 2AP1 CRT showing the distances from the screen to the middle of the deflection plate pairs.
Finally, calculate e/m = 8π2V / B2 L2 for each run and yield an average estimate for e/m. How well do your measurements compare with the accepted value of e/m = 1.76 × 1011 Coulomb/kg?
Leave a Reply