Material Balances and Energy Balances

Material balances, also called mass balances and energy balances, are applications of conservation of mass and energy to the analysis of physical systems. Process and equipment selections and sizing require a complete knowledge of all material and energy flow to and from each unit. By accounting for material and/or energy entering and leaving a system, mass and/or flows can be identified which might have been unknown or difficult to measure without this technique. The exact conservation law used in the analysis of the system depends on the context of the problem, but all revolve around mass and energy conservation, i.e. that matter or energy cannot be destroyed or created spontaneously (Haugen et al. 1954; Himmelblau 1998).

The general form quoted for a mass balance is the mass that enters a system must, by conservation of mass, either leave the system or accumulate within the system.

(3.21)

For a steady‐state operation, all operating parameters are time independent, and Eq. (3.21) becomes

(3.22)

Therefore, mass balances are used widely in engineering and environmental analyses. For example, mass balance theory is used to design chemical reactors, to analyze alternative processes to produce chemicals, as well as to model pollution dispersion and other processes of physical systems. In majority of cases, Eq. (3.21) describes material and energy balance around pollution control equipment that is designed for steady‐state operation. Some exceptions to this generalization are encountered in the design of incinerators, direct‐fired dryers, and adsorbers owing to the heat generation and/or pollutant accumulation within the units.

In environmental monitoring, the term budget calculations is used to describe mass balance equations where they are used to evaluate the monitoring data (comparing input and output, etc.) In biology the dynamic energy budget theory for metabolic organization makes explicit use of mass and energy balance.

The following steps are helpful in performing materials and energy balance calculations:

Draw a sketch of the process
Identify and label all entering and exiting streams
Label all pertinent data on the sketch
Draw a dashed envelope around that portion of the process involved in the balance
Select a suitable basis for the calculation.

EXAMPLE 3.15 A MASS BALANCE PROBLEM ON HAPS

A manufacturing company has, as part of their first audit, gathered the following data. Estimate the potential annual air emissions in kg of VOCs from the company.

Purchasing department records
Materials	Purchasing quantity (barrels)
Methylene chlorine (CH₂Cl₂)	228
Trichloroethylene (C₂HCl₃)	505

Wastewater treatment plant influent
Materials	Average concentration (mg/l)
CH₂Cl₂	4.04
C₂HCl₃	3.25
(Average flow into wastewater treatment plant is 0.076 m³/s)
Hazardous waste manifests
Materials	Barrels	Concentration
CH₂Cl₂	228	25
C₂HCl₃	505	80
Unused barrel at end of year
CH₂Cl₂	8
C₂HCl₃	13

SOLUTION

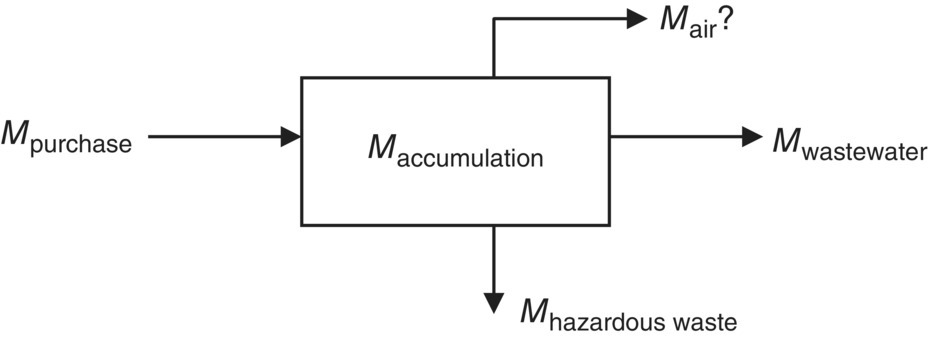
Diagram displaying a box labeled Maccumulation with arrows labeled Mpurchase, Mwastewater, Mhazardous waste, and Mair?.

The mass balance equation would be

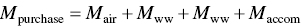
Solving this equation for M_air gives us the estimated VOC emission.

First, we calculate the mass purchased. The eternity of Earth compound is given below.

Mass purchased

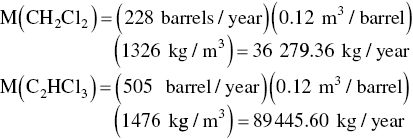
Now we calculate the mass received at the wastewater treatment plant (note that mg/l = g/m³).

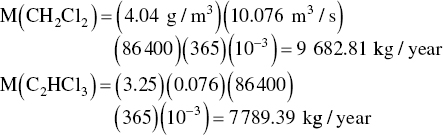
The mass shipped to the hazardous waste disposed facility is calculated next

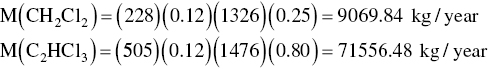
Accumulated

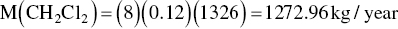
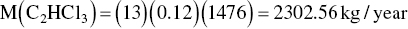
The estimated air emission for each compound is then

EXAMPLE 3.16 HEAT RECOVERY AND SAVE MONEY

Exhaust gas from a chemical process flows at a rate of 8000 acfm from point A at 250 °F and 1 atm pressure. It flows through a circular duct to a fan where the pressure is boosted to 4 inches of water (gage) and then flows to an incinerator. Fuel gas is burned at a rate of 75 lb/h and the temperature of the incinerator exhaust gas is 1200 °F. Assuming both the process exhaust and the incinerator exhaust streams have properties similar to air, calculate the enthalpy that has been added by burning the fuel gas (Btu/h). Assume that you can recover heat from the incinerator exhaust by buying a heat exchanger to cool the gases to 500 °F while recovering useful heat. Assuming that such heat is worth $7.00/million Btu, how much money could you save by recovering that amount of heat ($/day)?

Given:

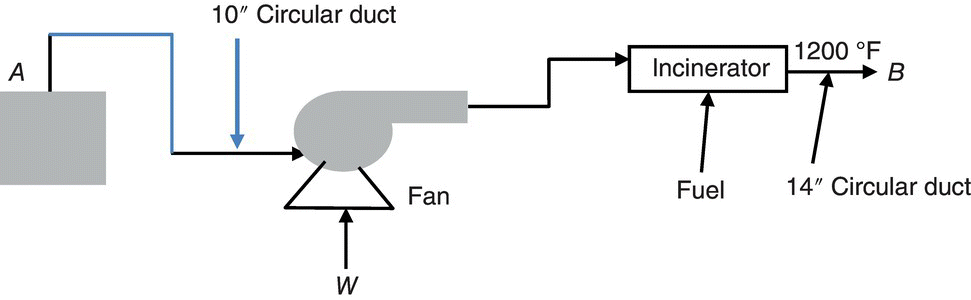
Diagram displaying a shaded box labeled A connecting to a triangle and shaded irregular shape for fan leading to a box labeled Incinerator, with arrows labeled 10” circular duct, fuel, W, and 14” circular duct.

Q = 8000 cfm
T₁ = (250 + 460)°R = 710 °R
T₂(1200 + 460)°R = 1.66 × 10³ °R
P = 1 atm = 2.12 × 10³ psf
R_c = (0.7302 atm ft³)/(mol. ^°R)
Fuel_Feed_Rate = 75 lb/h

SOLUTION

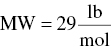
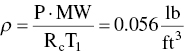
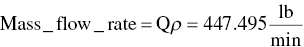
(From Table C.4)

Calculate mass flow rate from ideal gas law:

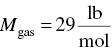
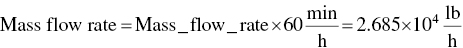
∆H_fuel = Mass flow rate × ∆H

Calculate value of recovered heat

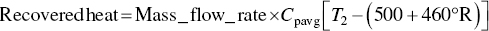
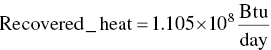
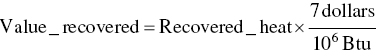
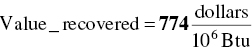
EXAMPLE 3.17 HAZARDOUS WASTE MASS BALANCE FOR MEETING REGULATORY CRITERION

A solvent distilling and recycling, which primarily recycles TCE, is under investigation for the toxic air emissions. As the hazardous waste manager at the site, your goal is to account for the solvents coming in and out into the facility using a waste audit based on a mass balance. The wastes coming into the facility over a one‐year period include the following:

Invoice number	Volume (l)	TCE concentration (mg/l)
204	10 000 000	130
205	5 000 000	210
206	5 000 000	200

These aqueous solutions were distilled to concentrate the TCE. The concentrated product was then shipped (over the same one‐year time period) from the facility in tanker trucks as 90% (900 g/l) formulations (the other 10% were various impurities):

Shipping no.	Volume (l)	TCE concentration (mg/l)
1021	2200	900
205	1400	9000

The state regulatory agency allows 200 kg/year TCE emitted into the air from your facility. Using a materials balance, show that the plant is meeting this regulatory criterion.

SOLUTION

Waste in (over a one‐year period):
Waste out (over a 1‐year period):

Therefore, volatile losses = 3350 – 3240 = 110 kg (over a one‐year period)

Answer: Because volatile losses are less than 200 kg/year, the plant is meeting the regulatory criterion.

EXAMPLE 3.18

A 600 MW coal‐fired power plant has an overall thermal efficiency of 38%. It is burning coal that has a heating value of 12 000 Btu/lb, an ash content of 5%, a sulfur content of 3.0%, and a CO₂ emission factor of 220 lb/million Btu. Calculate the heat emitted to the environment (Btu/s), the coal feed rate (T/day), the degree (%) of sulfur dioxide control needed to meet an emission standard of 0.15 lbSO₂/million Btu of heat input, and the CO₂ emission rate (MT/day).