In water-drive reservoirs, the relation between Gp and p/z is not linear, as can be seen by an inspection of Eqs. (4.13) and (4.16). Because of the water influx, the pressure drops less rapidly with production than under volumetric control, as shown in the upper curve of Fig. 4.2. Consequently, the extrapolation technique described for volumetric reservoirs is not applicable. Also, where there is water influx, the initial gas in place calculated at successive stages of depletion, assuming no water influx, takes on successively higher values, whereas with volumetric reservoirs the calculated values of the initial gas should remain substantially constant.
Equation (4.13) may be expressed in terms of the initial pore volume, Vi, by recognizing that Vi= GBgi and using Eq. (2.15) for Bg and Bgi:
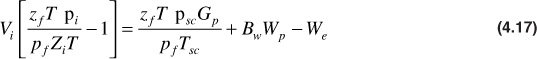
For volumetric reservoirs, discussed in the previous section, this equation can be reduced and rearranged to give

Examples 4.2, 4.3, and 4.4 illustrate the use of the various equations that we have described in gas reservoir calculations.
Example 4.2 Calculating the Initial Gas in Place and the Initial Reserve of a Gas Reservoir from Pressure-Production Data for a Volumetric Reservoir
Given
Base pressure = 15.025 psia
Initial pressure = 3250 psia
Reservoir temperature = 213°F
Standard pressure = 15.025 psia
Standard temperature = 60°F
Cumulative production = 1.00 × 109 SCF
Average reservoir pressure = 2864 psia
Gas deviation factor at 3250 psia = 0.910
Gas deviation factor at 2864 psia = 0.888
Gas deviation factor at 500 psia = 0.951
Solution
Solve Eq. (4.18) for the reservoir gas pore volume Vi:
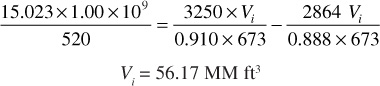
The initial gas in place by the real gas law is
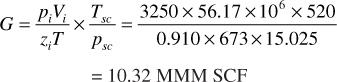
The gas remaining at 500-psia abandonment pressure is
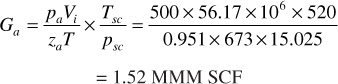
The initial gas reserve based on a 500-psia abandonment pressure is the difference between the initial gas in place and the gas remaining at 500 psia, or
Gr = G – Ga = (10.32 – 1.52) × 109
= 8.80 MMM SCF
Example 4.3 illustrates the use of equations to calculate the water influx when the initial gas in place is known. It also shows the method of estimating the residual gas saturation of the portion of the reservoir invaded by water, at which time a reliable estimate of the invaded volume can be made. This is calculated from the isopach map, the invaded volume being delineated by those wells that have gone to water production. The residual gas saturation calculated in Example 4.3 includes that portion of the lower permeability rock within the invaded area that actually may not have been invaded at all, the wells having been “drowned” by water production from the more permeable beds of the formation. Nevertheless, it is still interpreted as the average residual gas saturation, which may be applied to the uninvaded portion of the reservoir.
Example 4.3 Calculating Water Influx and Residual Gas Saturation in Water-Drive Gas Reservoirs
Given
Bulk reservoir volume, initial = 415.3 MM ft3
Average porosity = 0.172
Average connate water = 0.25
Initial pressure = 3200 psia
Bgi = 0.005262 ft3/SCF, 14.7 psia and 60°F
Final pressure = 2925 psia
Bgf = 0.005700 ft3/SCF, 14.7 psia and 60°F
Cumulative water production = 15,200 bbl (surface)
Bw = 1.03 bbl/surface bbl
Gp = 935.4 MM SCF at 14.7 psia and 60°F
Bulk volume invaded by water at 2925 psia = 13.04 MM ft3
Solution
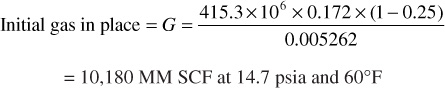
Substitute in Eq. (4.13) to find We:
We = 935.4 × 106 × 0.005700 – 10,180 × 106
(0.005700 – 0.005262) + 15,200 × 1.03 × 5.615
= 960,400 ft3
This much water has invaded 13.04 MM ft3 of bulk rock that initially contained 25% connate water. Then the final water saturation of the flooded portion of the reservoir is

Then the residual gas saturation Sgr is 33%.
Example 4.4 Using the p/z Plot to Estimate Cumulative Gas Production
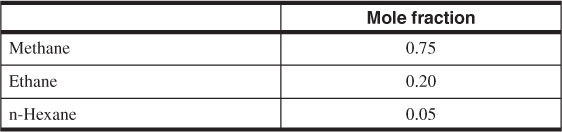
A dry gas reservoir contains gas of the following composition
The initial reservoir pressure was 4200 psia, with a temperature of 180°F. The reservoir has been producing for some time. Two pressure surveys have been made at different times:
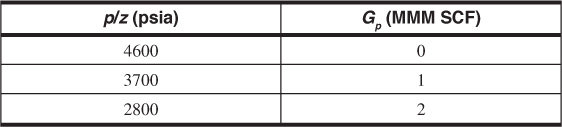
(a) What will be the cumulative gas produced when the average reservoir pressure has dropped to 2000 psia?
(b) Assuming the reservoir rock has a porosity of 12%, the water saturation is 30%, and the reservoir thickness is 15 ft, how many acres does the reservoir cover?
Solution
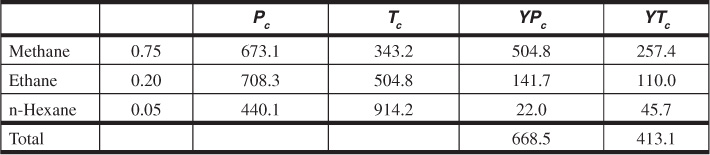
(a) To get Gp at 2000 psia, calculate z and the p/z. Use pseudocritical properties.
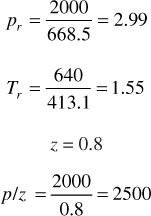
A linear regression of the data plotted in Fig. 4.3 yields the following equation for the best straight line through the data:
p/z = –9(10)–7Gp + 4600
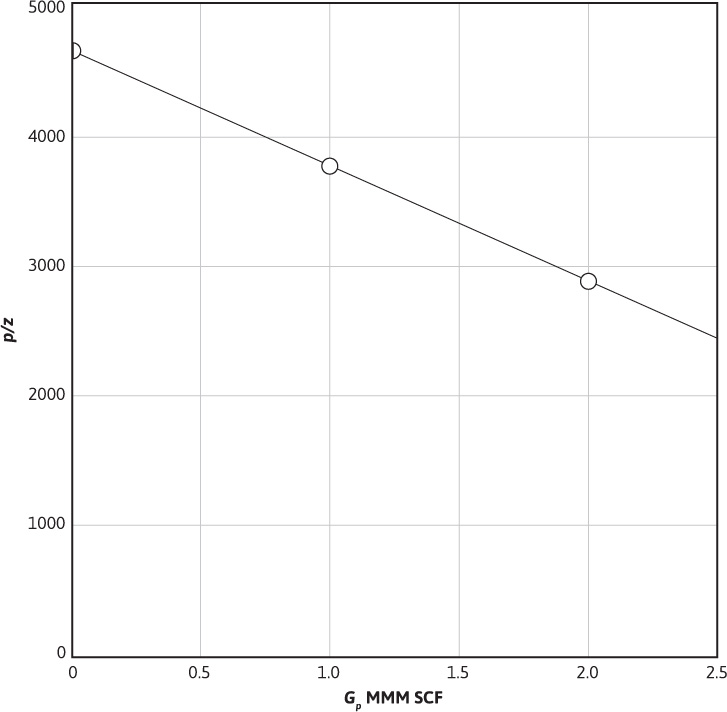
Figure 4.3 p/z versus Gp for Example 4.4.
Substituting a value of p/z = 2500 in this equation yields
2500 = –9(10)–7Gp + 4600
Gp = 2.33(10)9 SCF or 2.33 MMM SCF
(b) Substituting a value of p/z = 0 into the straight-line equation would yield the amount of produced gas if all of the initial gas were produced; therefore, the Gp at this p/z is equal to the initial gas in place.
0 = – 9(10)–7Gp + 4600
Gp (p/z = 0) = G = 5.11(10)9 SCF or 5.11 MMM SCF
Recognizing that Vi = GBgi and that Bgi = 0.02829(zi/pi)T,
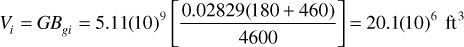
Also,
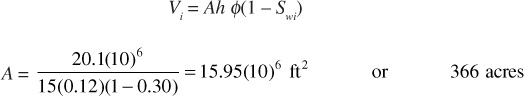
Leave a Reply