The material balance equation for undersaturated reservoirs was developed:
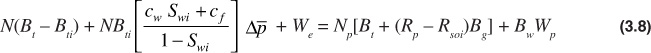
Neglecting the change in porosity of rocks with the change of internal fluid pressure, which is treated later, reservoirs with zero or negligible water influx are constant volume or volumetric reservoirs. If the reservoir oil is initially undersaturated, then initially it contains only connate water and oil, with their solution gas. The solubility of gas in reservoir waters is generally quite low and is considered negligible for the present discussion. Because the water production from volumetric reservoirs is generally small or negligible, it will be considered zero. From initial reservoir pressure down to the bubble point, then, the reservoir oil volume remains a constant, and oil is produced by liquid expansion. Incorporating these assumptions into Eq. (3.8), the following is obtained:
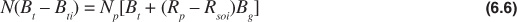
While the reservoir pressure is maintained above the bubble-point pressure and the oil remains undersaturated, only liquid will exist in the reservoir. Any gas that is produced on the surface will be gas coming out of solution as the oil moves up through the wellbore and through the surface facilities. All this gas will be gas that was in solution at reservoir conditions. Therefore, during this period, Rp will equal Rso and Rso will equal Rsoi, since the solution gas-oil ratio remains constant. The material balance equation becomes

This can be rearranged to yield fractional recovery, RF, as

The fractional recovery is generally expressed as a fraction of the initial stock-tank oil in place. The pressure-volume-temperature (PVT) data for the 3–A–2 reservoir of a field is given in Fig. 6.2.
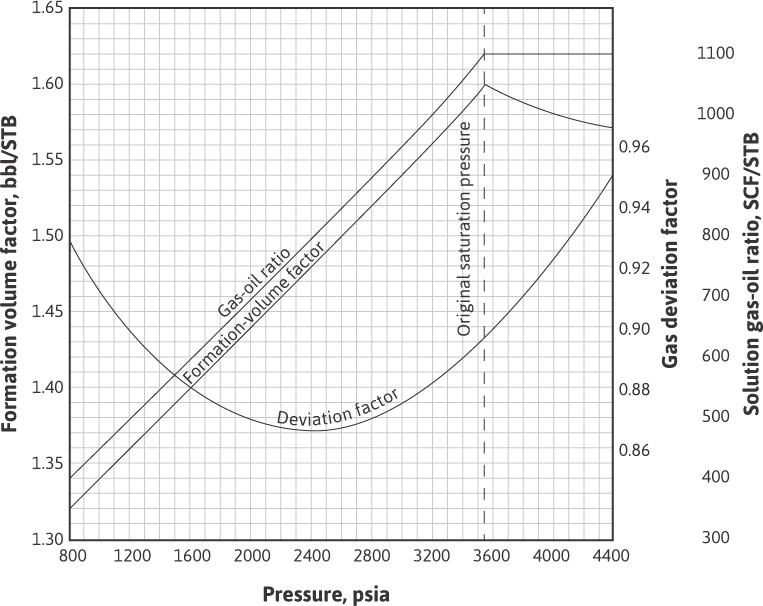
Figure 6.2 PVT data for the 3–A–2 reservoir at 190°F.
The formation volume factor plotted in Fig. 6.2 is the single-phase formation volume factor, Bo. The material balance equation has been derived using the two-phase formation volume factor, Bt. Bo and Bt are related by Eq. (2.29):

It should be apparent that Bt = Bo above the bubble-point pressure because Rso is constant and equal to Rsoi.
The reservoir fluid has an oil volume factor of 1.572 bbl/STB at the initial pressure 4400 psia and 1.600 bbl/STB at the bubble-point pressure of 3550 psia. Then, by volumetric depletion, the fractional recovery of the stock-tank oil at 3550 psia by Eq. (6.8) is
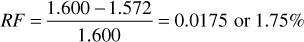
If the reservoir produced 680,000 STB when the pressure dropped at 3550 psia, then the initial oil in place by Eq. (6.7) is
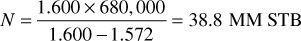
Below 3550 psia, a free gas phase develops; and for a volumetric, undersaturated reservoir with no water production, the hydrocarbon pore volume remains constant, or

Figure 6.3 shows schematically the changes that occur between initial reservoir pressure and some pressure below the bubble point. The free-gas phase does not necessarily rise to form an artificial gas cap, and the equations are the same if the free gas remains distributed throughout the reservoir as isolated bubbles. Equation (6.6) can be rearranged to solve for N and the fractional recovery, RF, for any undersaturated reservoir below the bubble point.

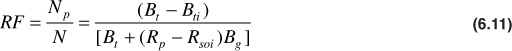
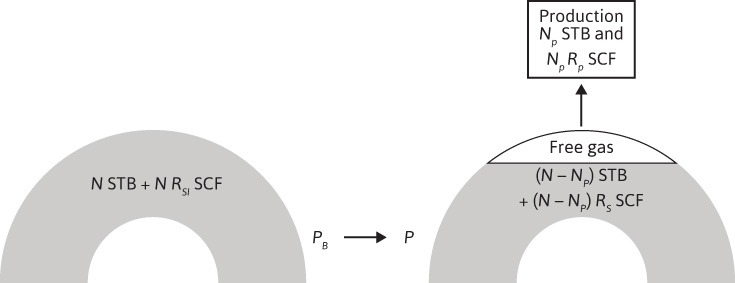
Figure 6.3 Diagram showing the formation of a free-gas phase in a volumetric reservoir below the bubble point.
The net cumulative produced gas-oil ratio (Rp) is the quotient of all the gas produced from the reservoir (Gp) and all the oil produced (Np). In some reservoirs, some of the produced gas is returned to the same reservoir, so that the net produced gas is only that which is not returned to the reservoir. When all the produced gas is returned to the reservoir, Rp is zero.
An inspection of Eq. (6.11) indicates that all the terms except the produced gas-oil ratio (Rp) are functions of pressure only and are the properties of the reservoir fluid. Because the nature of the fluid is fixed, it follows that the fractional recovery RF is fixed by the PVT properties of the reservoir fluid and the produced gas-oil ratio. Since the produced gas-oil ratio occurs in the denominator of Eq. (6.11), large gas-oil ratios give low recoveries and vice versa.
Example 6.1 Calculating the Effect of the Produced Gas-Oil Ratio (Rp) on Fractional Recovery in Volumetric, Undersaturated Reservoirs
Given
The PVT data for the 3–A–2 reservoir (Fig. 6.2)
Cumulative GOR at 2800 psia = 3300 SCF/STB
Reservoir temperature = 190°F = 650°R
Standard conditions = 14.7 psia and 60°F
Solution
The following values are determined graphically from Fig 6.2. Rsoi is the GOR at the initial reservoir condition of p = 4400 psia and Rsoi = 1100 SCF/STB. Boi is the formation volume factor at initial reservoir conditions of p = 4400 psia and Boi = 1.572 bbl/STB. At 2800 psia, Rso is the GOR at 900 SCF/STB and Bo is the formation volume factor at 1.520 bbl/STB. Rp was given as the cumulative GOR at 2800 psia. Bg and Bt at 2800 psia are calculated as follows from Eqs. (2.16) and (2.29):
Rsoi = 1100 SCF/STB Boi = 1.572 bbl/STB
Rso at 2800 psia = 900 SCF/STB Bo at 2800 psia = 1.520 bbl/STB
Rp = 3300 SCF/STB
Bt = Bo + Bg(Rsoi – Rso)
Bt = 1.520 + 0.00102(1100 – 900) = 1.724 bbl/STB
Then, using Eq. (6.11) at 2800 psia,

If two-thirds of the produced gas had been returned to the reservoir, at the same pressure (i.e., 2800 psia), Rp would be 1100 SCF/STB and the fractional recovery would have been

Equation (6.10) may be used to find the initial oil in place. For example, if 1.486 MM STB had been produced down to 2800 psia, for Rp = 3300 SCF/STB, the initial oil in place is
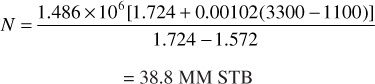
The calculations of Example 6.1 for the 3–A–2 reservoir show that, for Rp = 3300 SCF/STB, the recovery at 2800 psia is 3.83% and that, if Rp had been only 1100 SCF/STB, the recovery would have been 8.80%. Neglecting in each case the 1.75% recovery by liquid expansion down to the bubble-point pressure, the effect of reducing the gas-oil ratio by one-third is approximately to triple the recovery. The produced gas-oil ratio can be controlled by working over high gas-oil ratio wells, by shutting in or reducing the producing rates of high ratio wells, and/or by returning some or all of the produced gas to the reservoir. If gravitational segregation occurs during production so that a gas cap forms, as shown in Fig. 6.3, and if the producing wells are completed low in the formation, their gas-oil ratios will be lower and recovery will be improved. Simply from the material balance point of view, by returning all produced gas to the reservoir, it is possible to obtain 100% recoveries. From the point of view of flow dynamics, however, a practical limit is reached when the reservoir gas saturation rises to values in the range of 10% to 40% because the reservoir becomes so permeable to gas that the returned gas moves rapidly from the injection wells to the production wells, displacing with it only a small quantity of oil. Thus although gas-oil ratio control is important in solution gas-drive reservoirs, recoveries are inherently low because the gas is produced faster than the oil. Outside the energy stored up in the liquid above the bubble point, the energy for producing the oil is stored up in the solution gas. When this gas has been produced, the only remaining natural source of energy is gravity drainage, and there may be a considerable period in which the oil drains downward to the wells from which it is pumped to the surface.
In the next section, a method is presented that allows the material balance equation to be used as a predictive tool. The method was used by engineers performing calculations on the Canyon Reef Reservoir in the Kelly-Snyder Field.
Leave a Reply