Consider an elemental plate of thickness dy at a distance y from the diametral axis as shown in Figure 11.24. Radius of this elemental circular plate x is given by,
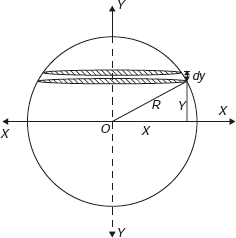
Figure 11.24 Mass Moment of Inertia of Sphere
x2 = R2 − y2
Mass of the elemental plate, dm = ρπx2 dy = ρπ (R2 − y2)dy
Moment of inertia of the plate element about axis
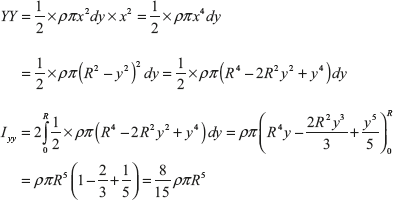
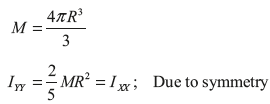
Mass moment of inertia of hemisphere about the axis ZZ,
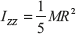
Moment of inertia of the plane element about the axis
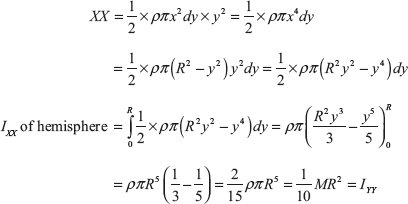
Leave a Reply