Let in Figure 11.23, Ro = Outer radius of cylinder; Ri = Inner radius of the cylinder, L = Length of cylinder; ρ = Mass density of the cylinder; and M = Mass of the cylinder.
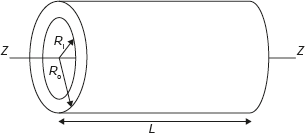
Figure 11.23 Mass Moment of Inertia of a Hollow Cylinder
Consider a small elemental ring of width dr at a distance of radius r from the centre of cylinder then the mass of the element, dm = ρ·2πr·dr·L
Now mass moment of inertia of the element about the axis ZZ
IZZelement = (ρ × 2πrdr × L)× r2
Moment of inertia of the cylinder about the axis ZZ
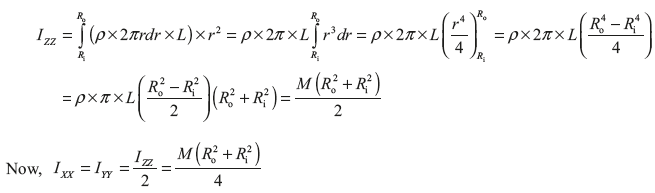
Leave a Reply